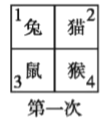
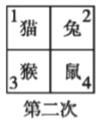
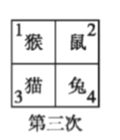
题目内容
【题目】如图,在四棱锥
中,
是等边三角形,
,
,
.
(Ⅰ)求证: 
(Ⅱ)若平面
平面
,
,求二面角
的余弦值
【答案】（1）见解析；（2）
.
【解析】分析：第一问要证明的是线线垂直，在做题的过程中，需要用到平面四边形中平行四边形的性质以及勾股定理得到线线垂直，之后应用线面垂直的判定定理得到线面垂直，之后应用线面垂直的性质，得到线线垂直；第二问利用题中的条件，得到相应的垂直关系，建立相应的空间直角坐标系，利用法向量求得二面角的余弦值.
详解：（Ⅰ）取
的中点
，连接
为等边三角形
且
又
四边形
为矩形
, 
平面
又 
平面， 
(Ⅱ)由（Ⅰ）知
平面
平面
，平面
平面
，
平面
平面,
以为坐标原点，以
所在方向分别为
轴，
轴，
轴的正方向，建立空间直角坐标系
设
则
, 
,
又
，得
,
,
,
,
设平面
法向量
由
,得
，取
，得
又知
是平面的一个法向量，设
二面角
的余弦值为.
阅读快车系列答案【题目】某校为了探索一种新的教学模式，进行了一项课题实验，甲班为实验班，乙班为对比班，甲乙两班的人数均为50人，一年后对两班进行测试，测试成绩的分组区间为
80,90
、90,100、100,110、110,120、120,130，由此得到两个班测试成绩的频率分布直方图：
（1）完成下面2×2列联表，你能有97.5
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗？并说明理由；
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 |
|
| 50 |
乙班 |
|
| 50 |
合计 |
|
| 100 |
（2）根据所给数据可估计在这次测试中，甲班的平均分是105.8，请你估计乙班的平均分，并计算两班平均分相差几分？
附：
，其中
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
【题目】为加快新能源汽车产业发展，推进节能减排，国家对消费者购买新能源汽车给予补贴，其中对纯电动乘用车补贴标准如下表：
新能源汽车补贴标准 | |||
车辆类型 | 续驶里程R（公里） | ||
80≤R＜150 | 150≤R＜250 | R≥250 | |
纯电动乘用车 | 3.5万元/辆 | 5万元/辆 | 6万元/辆 |
某校研究性学习小组，从汽车市场上随机选取了M辆纯电动乘用车，根据其续驶里程R（单次充电后能行驶的最大里程）作出了频率与频数的统计表：
分组 | 频数 | 频率 |
80≤R＜150 | 2 | 0.2 |
150≤R＜250 | 5 | x |
R≥250 | y | z |
合计 | M | 1 |
（Ⅰ）求x，y，z，M的值；
（Ⅱ）若从这M辆纯电动乘用车中任选2辆，求选到的2辆车续驶里程都不低于150公里的概率；
（Ⅲ）若以频率作为概率，设X为购买一辆纯电动乘用车获得的补贴，求X的分布列和数学期望EX．
