题目内容

11．已知f（x）=ax5+bx3+cx-8，且f（-2）=10，则f（2）=-26．

分析 将f（x）=ax5+bx3+cx-8，转化为f（x）+8=ax5+bx3+cx，则F（x）=f（x）+8为奇函数，利用奇函数的性质求f（2）即可．

解答 解：由f（x）=ax5+bx3+cx-8，得f（x）+8=ax5+bx3+cx，
设F（x）=f（x）+8，
则F（x）为奇函数，
∴F（-2）=-F（2），
即f（-2）+8=-f（2）-8，
∴f（2）=-f（-2）-16=-10-16=-26，
故答案为：-26．

点评 本题主要考查函数奇偶性的应用和求解，利用函数特点构造奇函数是解决本题的关键，本题也可以直接建立方程组进行求解．

练习册系列答案
相关题目
1．如果圆（x+3）2+（y-1）2=1关于直线l：mx+4y-1=0对称，则直线l的斜率为（　　）
A．4B．-4C．$\frac{1}{4}$D．-$\frac{1}{4}$
2．设m∈N*，已知函数f（x）=（2m-m2）•x${\;}^{2{m}^{2}+3m-4}$在（0，+∞）上是增函数．
（1）求函数f（x）的解析式；
（2）设g（x）=$\frac{[f（x）]^{2}+{λ}^{2}}{f（x）}$（λ≠0是常数），试讨论g（x）在（-∞，0）上的单调性，并求g（x）在区间（-∞，0）上的最值．
19．a、b表示两条直线，α、β、γ表示三个平面，下列命题中错误的是（　　）
A．a?α，b?α，且a∥β，b∥β，则α∥β
B．a、b是异面直线，则存在唯一的平面与a、b等距
C．a⊥α，b?β，a⊥b，则α∥β
D．α⊥γ，γ∥β，a⊥α，b⊥β，则a⊥b
6．下列各组函数是相等函数的是（　　）
A．y=$\frac{|x|}{x}$与 y=1B．y=$\frac{{x}^{3}+x}{{x}^{2}+1}$与y=x
C．y=x与y=（$\sqrt{x}$）2D．y=|x|与y=$\left\{\begin{array}{l}{x，x＞1}\\{-x，x＜1}\end{array}\right.$
16．已知函数f（x）=loga[（a-1）x-1]．
（1）求函数f（x）的定义域；
（2）若对任意x∈[2，+∞）恒有f（x）＞0，试确定a的取值范围．
3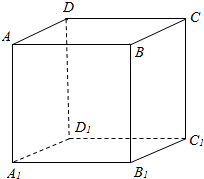．在正方体ABCD-A1B1C1D1的棱所在的直线中，与直线AB垂直的异面直线共有（　　）
A．1条B．2条C．4条D．8条
20．点P（x0，y0）是圆C：x2+y2=1上的一个动点，过点P的直线l与圆C相切
（1）求证：直线l的方程为x0x+y0y=1；
（2）若直线l与x轴、y轴的交点分别为点A、B，且|PB|，|PA|，|AB|成等比数列，求点P的坐标．
1．已知函数f（x）=k-$\frac{2}{{2}^{x}+1}$，k∈R．
（1）是否存在实数k使得函数f（x）为奇函数？若存在，求出实数k；若不存在，请说明理由；
（2）判断函数f（x）的单调性，并证明你的判断；
（3）当k=1时，若不等式f（t2-2t）+f（2t2-m）＞0对于t∈R恒成立，求实数m的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网