题目内容
【题目】已知函数f(x)是定义在R上的奇函数,且当x≥0时,f(x)=![]() .
.
(1)求f(x)的解析式;
(2)判断f(x)的单调性;
(3)若对任意的t∈R,不等式f(k-3t2)+f(t2+2t)≤0恒成立,求k的取值范围.
【答案】(1)f(x)=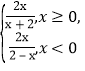 ;(2) f(x)在(-∞,+∞)上是增函数; (3)k≤-
;(2) f(x)在(-∞,+∞)上是增函数; (3)k≤-![]() .
.
【解析】
(1)当x<0时,f(x)=-f(-x)=-![]() =
=![]() .即得f(x)的解析式. (2)先分析得到 f(x)在[0,+∞)上是增函数.又f(x)是奇函数,所以f(x)在(-∞,+∞)上是增函数.(3)利用函数的奇偶性和单调性得到k-3t2≤-t2-2t,即2t2-2t-k≥0,解Δ=4+8k≤0,即得解.
.即得f(x)的解析式. (2)先分析得到 f(x)在[0,+∞)上是增函数.又f(x)是奇函数,所以f(x)在(-∞,+∞)上是增函数.(3)利用函数的奇偶性和单调性得到k-3t2≤-t2-2t,即2t2-2t-k≥0,解Δ=4+8k≤0,即得解.
(1)因为当x≥0时,f(x)=![]() ,
,
所以当x<0时,f(x)=-f(-x)=-![]() =
=![]() .
.
所以f(x)=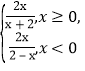
(2)当x≥0时,f(x)=![]() =2-
=2-![]() ,
,
所以f(x)在[0,+∞)上是增函数.
又f(x)是奇函数,所以f(x)在(-∞,+∞)上是增函数.
(3)由题知不等式f(k-3t2)+f(t2+2t)≤0等价于
f(k-3t2)≤f(-t2-2t),
又f(x)在(-∞,+∞)上是增函数,
所以k-3t2≤-t2-2t,即2t2-2t-k≥0,
即对一切t∈R,恒有2t2-2t-k≥0,
所以Δ=4+8k≤0,解得k≤-![]() .
.

练习册系列答案
相关题目