��Ŀ����
����Ŀ����֪�����з��д�С����״��ͬ��С�����ɣ����б��Ϊ0��С��1�������Ϊ1��С��1�������Ϊ2��С��![]() ��.���Ӵ����������ȡ1��С��ȡ�����Ϊ2��С��ĸ�����
��.���Ӵ����������ȡ1��С��ȡ�����Ϊ2��С��ĸ�����![]() .
.
��1����![]() ��ֵ��
��ֵ��
��2���Ӵ������зŻص������ȡ2��С�ǵ�һ��ȡ����С����Ϊ![]() ���ڶ���ȡ����С����Ϊ
���ڶ���ȡ����С����Ϊ![]() .
.
�ټǡ�![]() ��Ϊ�¼�
��Ϊ�¼�![]() �����¼�
�����¼�![]() �ĸ��ʣ�
�ĸ��ʣ�
��������![]() ����ȡ2��ʵ��
����ȡ2��ʵ��![]() �����¼���
�����¼���![]() ��������ĸ���.
��������ĸ���.
���𰸡���1��2����2����![]() ����
����![]()
�������������������1�����ôӴ����������ȡ1��С��ȡ�������2��С��ĸ�����![]() ��ȷ��n��ֵ��
��ȷ��n��ֵ��
��2����i���Ӵ������зŻص������ȡ2�����л����¼�16����������a+b=2��Ϊ�¼�A�Ļ����¼���5�����ʿ�����ʣ�
��ii������![]() �������Ϊ�¼�B�����¼�
�������Ϊ�¼�B�����¼�![]() �ȼ��ڡ�
�ȼ��ڡ�![]() ���������
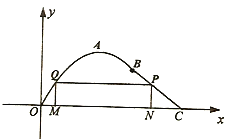
��������� ![]() ���Կ���ƽ���еĵ�����꣬ȷ��ȫ����������ɵ������¼�B���ɵ��������ü��θ��Ϳ���ý��ۣ�
���Կ���ƽ���еĵ�����꣬ȷ��ȫ����������ɵ������¼�B���ɵ��������ü��θ��Ϳ���ý��ۣ�
���������
��1��������![]() ����
����![]() .
.
�ټDZ��Ϊ0��С��Ϊ![]() �����Ϊ1��С��Ϊ
�����Ϊ1��С��Ϊ![]() �����Ϊ2��С��Ϊ
�����Ϊ2��С��Ϊ![]() ����ȡ��2��С��Ŀ�������У�
����ȡ��2��С��Ŀ�������У� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��16�֣��������㡰
��16�֣��������㡰![]() ������5�֣�
������5�֣� ![]() .�����������Ϊ
.�����������Ϊ![]()
�ڼǡ�![]() �������Ϊ�¼�
�������Ϊ�¼�![]() �����¼�
�����¼�![]() �ȼ��ڡ�
�ȼ��ڡ�![]() ���������
��������� ![]() ���Կ���ƽ���еĵ�����꣬��ȫ����������ɵ�����Ϊ
���Կ���ƽ���еĵ�����꣬��ȫ����������ɵ�����Ϊ![]() �����¼�
�����¼�![]() ���ɵ�����Ϊ
���ɵ�����Ϊ![]() .��������ĸ���Ϊ
.��������ĸ���Ϊ![]()

 �»����ܶ�Ա��ϵ�д�
�»����ܶ�Ա��ϵ�д� ����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�
����ͼ����ּ��������ҵ֣�ݴ�ѧ������ϵ�д�����Ŀ�����Ż������ķ�չ���ƶ�֧��![]() �ֳ��ֻ�֧��
�ֳ��ֻ�֧��![]() ����������Ⱥ�ڵ�����
����������Ⱥ�ڵ�����![]() ijѧУ��ȤС��Ϊ���˽��ƶ�֧��������Ⱥ���е���֪�ȣ���
ijѧУ��ȤС��Ϊ���˽��ƶ�֧��������Ⱥ���е���֪�ȣ���![]() �����Ⱥ����������飬��������������ʹ���ƶ�֧���������У��ش��������Ĺ���50���ˣ�����50���˰�������ֳ�5�飬�����Ƴ�Ƶ�ʷֲ���
�����Ⱥ����������飬��������������ʹ���ƶ�֧���������У��ش��������Ĺ���50���ˣ�����50���˰�������ֳ�5�飬�����Ƴ�Ƶ�ʷֲ���![]() ��������ģ������
��������ģ������![]() �����
�����
���� | Ƶ�� | Ƶ�� | |
��1�� |
| 10 |
|
��2�� |
|
|
|
��3�� |
| 15 |
|
��4�� |
|
|
|
��5�� |
| 2 |
|
�ϼ� | 50 |
| |
![]() ����
����![]() �������ݷֱ��Ƕ��٣�
�������ݷֱ��Ƕ��٣�
![]() �ӵ�1�飬��3�飬��4�����÷ֲ�����ķ�����ȡ6�ˣ���ÿ���ȡ��������
�ӵ�1�飬��3�飬��4�����÷ֲ�����ķ�����ȡ6�ˣ���ÿ���ȡ��������
![]() ��
��![]() ��ȡ��6�����������ȡ2�ˣ�������ȡ��2������ͬһ����ĸ��ʣ�
��ȡ��6�����������ȡ2�ˣ�������ȡ��2������ͬһ����ĸ��ʣ�