题目内容
7.已知复数z=1-i(i是虚数单位),函数f(x)=|2x+1|-|x-4|.(Ⅰ)若${z^2}+a\overline z+b=3-3i$,求实数a,b的值;
(Ⅱ)解不等式f(x)>$\frac{b}{2}$.
分析 (Ⅰ)求出z2,然后利用${z^2}+a\overline z+b=3-3i$,利用复数相等的充要条件列出方程组求解即可.
(Ⅱ)转化|2x+1|-|x-4|>2,通过令y=|2x+1|-|x-4|,画出函数的图象,然后求解不等式的解.
解答 解:(Ⅰ)复数z=1-i,z2=(1-i)2=-2i,…(1分)
由${z^2}+a\overline z+b=3-3i$,得-2i+a(1+i)+b=3-3i,…(2分)
即(a+b)+(a-2)i=3-3i,所以$\left\{{\begin{array}{l}{a+b=3}\\{a-2=-3}\end{array}}\right.$,解得a=-1,b=4; …(6分)
(Ⅱ)由(1)知,b=4.所以f(x)=|2x+1|-|x-4|>2…(7分)
令y=|2x+1|-|x-4|,则$y=\left\{\begin{array}{l}-x-5,x≤-\frac{1}{2}\\ 3x-3,-\frac{1}{2}<x<4\\ x+5,x≥4\end{array}\right.$…(10分)
作出函数y=|2x+1|-|x-4|的图象,它与直线y=2的交点为(-7,2)和$({\frac{5}{3},2})$.…(1分)
所以|2x+1|-|x-4|>2的解集为$\{x\left|{x<-7或x>\frac{5}{3}\}}\right.$…(12分)
注:用零点分区间法相应给分.
点评 本题考查绝对值不等式的解法,数形结合的应用,复数的基本运算,考查计算能力以及作图能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.若下表数据对应的y关于x的线性回归方程为$\hat y=0.7x+a$,则a=0.35.
| x | 3 | 4 | 5 | 6 |
| y | 2.5 | 3 | 4 | 4.5 |
19.某射击运动员射击一次,命中目标的概率为0.8,问他连续射击两次都没命中的概率为( )
| A. | 0.8 | B. | 0.64 | C. | 0.16 | D. | 0.04 |
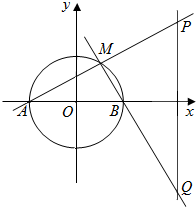 在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.
在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.