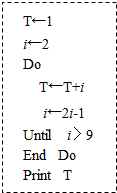题目内容
14.已知函数f(x)的定义域为[-2,2],若对于任意的x,y∈[-2,2],都有f(x+y)=f(x)+f(y),且当x>0时,有f(x)>0.(Ⅰ)证明:f(x)为奇函数;
(Ⅱ)判断f(x)在[-2,2]上的单调性,并证明;
(Ⅲ)设f(1)=1,若f(x)<logam(a>0且a≠1)对?x∈[-2,2]恒成立,求实数m的取值范围.
分析 (Ⅰ)令x=y=0可得f(0)=0,令y=-x及奇函数的定义即得证;
(Ⅱ)根据函数单调性的定义即可判断f(x)在[-2,2]上的单调性,并证明;
(Ⅲ)结合函数单调性和奇偶性的性质以及对数函数的性质将不等式恒成立进行转化即可得到结论.
解答 解:(Ⅰ)令x=y=0可得f(0)=0,
令y=-x则f(0)=f(x)+f(-x)=0,
即f(-x)=-f(x),则函数f(x)是奇函数.
(Ⅱ)f(x)在[-2,2]上为单调递增函数.…(5分)
任取-2≤x1<x2≤2,
则f(x1)-f(x2)=f(x1)-f[(x2-x1)+x1]=f(x1)-[f(x2-x1)+f(x1)]=-f(x2-x1),
因为当x>0时,f(x)>0,且x2-x1>0,
所以f(x2-x1)<0,
所以f(x1)-f(x2)<0,即f(x1)<f(x2).
所以函数f(x)在[-2,2]上为单调递增函数.…(8分)
( III )因为f(x)在[-2,2]上为单调递增函数,
所以f(x)max=f(2)=f(1+1)=f(1)+f(1)=2,
若f(x)<logam(a>0且a≠1)对?x∈[-2,2]恒成立,
则等价为f(x)max<logam(a>0且a≠1)对?x∈[-2,2]恒成立,
即2<logam(a>0且a≠1)对?x∈[-2,2]恒成立,
若a>1,则m>a2,此时实数m的取值范围是(a2,+∞),
若0<a<1,则0<m<a2,此时实数m的取值范围是(0,a2).
点评 本题主要考查抽象函数的应用,以及函数奇偶性和单调性的判断和应用,利用定义法是解决本题的关键.

练习册系列答案
相关题目
4.从2010名学生中选50人组成参观团,先用简单随机抽样方法剔除10人,再将其余2000人从0到1999编号,按等距系统抽样方法选取,若第一组采用抽签法抽到的号码是30,则最后一组入选的号码是( )
| A. | 1990 | B. | 1991 | C. | 1989 | D. | 1988 |
9.已知集合A={x|x2-2x-3≤0},B={x|-2≤x<2},则A∪B=( )
| A. | [-2,3] | B. | [-3,2] | C. | [-1,2] | D. | [-1,2) |
19.某射击运动员射击一次,命中目标的概率为0.8,问他连续射击两次都没命中的概率为( )
| A. | 0.8 | B. | 0.64 | C. | 0.16 | D. | 0.04 |
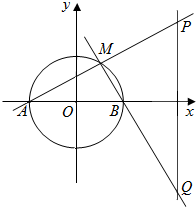 在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.
在平面直角坐标系xOy中,圆O:x2+y2=4交x轴于点A,B(点A在x轴的负半轴上),点M为圆O上一动点,MA,MB分别交直线x=4于P,Q两点.