题目内容
6.数列{an}满足nan+1-(n+1)an=0,已知a1=2.(I)求数列{an}的通项公式;
(Ⅱ)若bn=$\frac{1}{4}{a_{2n}}{a_{2n+1}}$,bn的前n项和为Sn,求证:Sn<$\frac{1}{3}$.
分析 (I)通过nan+1=(n+1)an可得$\frac{{a}_{n+1}}{n+1}$=2,进而可得结论;
(II)通过an=2n可得bn=2n(2n+1),放缩即得$\frac{1}{{b}_{n}}$<$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),并项相加即得结论.
解答 (I)解:∵nan+1=(n+1)an,
∴$\frac{{{a_{n+1}}}}{n+1}=\frac{a_n}{n}=\frac{a_1}{1}=2$,
∴an+1=2(n+1),∴an=2n;
(II)证明:∵an=2n,∴a2n=4n,a2n+1=2(2n+1),
∴${b_n}=\frac{1}{4}4n•2(2n+1)=2n(2n+1)$,
∴$\frac{1}{b_n}=\frac{1}{2n(2n+1)}<\frac{1}{(2n-1)(2n+1)}=\frac{1}{2}(\frac{1}{2n-1}-\frac{1}{2n+1})$,
∴${S_n}=\frac{1}{b_1}+\frac{1}{b_2}+…+\frac{1}{b_n}≤\frac{1}{6}+\frac{1}{2}(\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+…+\frac{1}{2n-1}-\frac{1}{2n+1})$
=$\frac{1}{3}-\frac{1}{4n+2}<\frac{1}{3}$(n∈N*).
点评 本题考查求数列的通项及数列的和的范围,利用放缩法及并项相加法是解决本题的关键,注意解题方法的积累,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知集合A={(x,y)|y2=4x},B={(x,y)|y=x+1},则A∩B=( )
| A. | {(1,-2)} | B. | {(1,2)} | C. | (1,2) | D. | (1,-2) |
18.已知函数f(x)=tan(2x-$\frac{π}{3}$),则下列说法错误的是( )
| A. | 函数f(x)的周期为$\frac{π}{2}$ | |
| B. | 函数f(x)的值域为R | |
| C. | 点($\frac{π}{6}$,0)是函数f(x)的图象一个对称中心 | |
| D. | f($\frac{2π}{5}$)<f($\frac{3π}{5}$) |
15.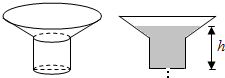 如图,一个旋转体沙漏,上部为一倒立圆台,下部为一圆柱,假定单
如图,一个旋转体沙漏,上部为一倒立圆台,下部为一圆柱,假定单
位时间流出的沙量固定,并且沙的上表面总能保持平整,设沙漏内剩
余沙的高度h与时间t的函数为h=f(t),则最接近f(t)的图象的是( )
 如图,一个旋转体沙漏,上部为一倒立圆台,下部为一圆柱,假定单
如图,一个旋转体沙漏,上部为一倒立圆台,下部为一圆柱,假定单位时间流出的沙量固定,并且沙的上表面总能保持平整,设沙漏内剩
余沙的高度h与时间t的函数为h=f(t),则最接近f(t)的图象的是( )
| A. | 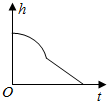 | B. | 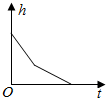 | C. | 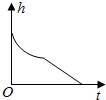 | D. | 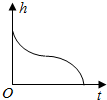 |
16.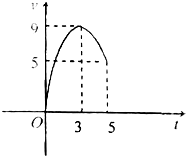 某校举行玩具机器人竞速比赛,要求参赛的机器人在规定的轨道中前行5秒钟,以运动路程的长短来决定比赛成绩.已知某参赛玩具机器人的运动速度v(单位:米/秒)和时间t(单位:秒)满足的关系大致如图所示,那么该玩具机器人运动5秒钟后,行驶的路程s(单位:米)可以是( )
某校举行玩具机器人竞速比赛,要求参赛的机器人在规定的轨道中前行5秒钟,以运动路程的长短来决定比赛成绩.已知某参赛玩具机器人的运动速度v(单位:米/秒)和时间t(单位:秒)满足的关系大致如图所示,那么该玩具机器人运动5秒钟后,行驶的路程s(单位:米)可以是( )
 某校举行玩具机器人竞速比赛,要求参赛的机器人在规定的轨道中前行5秒钟,以运动路程的长短来决定比赛成绩.已知某参赛玩具机器人的运动速度v(单位:米/秒)和时间t(单位:秒)满足的关系大致如图所示,那么该玩具机器人运动5秒钟后,行驶的路程s(单位:米)可以是( )
某校举行玩具机器人竞速比赛,要求参赛的机器人在规定的轨道中前行5秒钟,以运动路程的长短来决定比赛成绩.已知某参赛玩具机器人的运动速度v(单位:米/秒)和时间t(单位:秒)满足的关系大致如图所示,那么该玩具机器人运动5秒钟后,行驶的路程s(单位:米)可以是( )| A. | 25 | B. | $\frac{55}{2}$ | C. | $\frac{100}{3}$ | D. | 45 |