题目内容
8.已知正数a,b满足a+3b=5ab,实数x,y满足$\left\{\begin{array}{l}{x-y≤2}\\{x+2y≥5}\\{y-2≤0}\end{array}\right.$,若z=ax+by,求当3a+4b取最小值时z的最大值.分析 利用基本不等式求出a,b,然后由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,联立方程组求得最优解的坐标,代入目标函数得答案.
解答 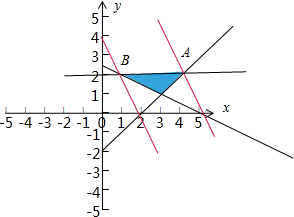 解:正数a,b满足a+3b=5ab,可得:$\frac{1}{b}+\frac{3}{a}=5$,则3a+4b=$\frac{1}{5}$(3a+4b)($\frac{1}{b}+\frac{3}{a}$)=$\frac{1}{5}$($\frac{3a}{b}+\frac{12b}{a}$+13)
解:正数a,b满足a+3b=5ab,可得:$\frac{1}{b}+\frac{3}{a}=5$,则3a+4b=$\frac{1}{5}$(3a+4b)($\frac{1}{b}+\frac{3}{a}$)=$\frac{1}{5}$($\frac{3a}{b}+\frac{12b}{a}$+13)
≥$\frac{1}{5}×(2\sqrt{\frac{3a}{b}×\frac{12b}{a}}+13)$=3,当且仅当a=1,b=$\frac{1}{2}$,取等号.
由约束条件$\left\{\begin{array}{l}x-y≤2\\ x+2y≥5\\ y-2≤0\end{array}\right.$作出可行域如图,
联立$\left\{\begin{array}{l}x-y=2\\ y-2=0\end{array}\right.$,解得A(4,2),
由z=x+$\frac{1}{2}$y,得y=-2x+2z,
由图可知,当直线y=-2x+2z过点A(4,2)时,直线在y轴上的截距最大,z有最大值为:4+2×$\frac{1}{2}$=5.
点评 本题考查了基本不等式的应用,简单的线性规划,考查了数形结合的解题思想方法,是中档题.

练习册系列答案
相关题目
18.已知函数f(x)=tan(2x-$\frac{π}{3}$),则下列说法错误的是( )
| A. | 函数f(x)的周期为$\frac{π}{2}$ | |
| B. | 函数f(x)的值域为R | |
| C. | 点($\frac{π}{6}$,0)是函数f(x)的图象一个对称中心 | |
| D. | f($\frac{2π}{5}$)<f($\frac{3π}{5}$) |
 某校计划在一块空地上建造一个面积为1800m2的矩形游泳池(如图所示),它的两边都留有宽6m的休息台,顶部和底部都留有宽为3m的人行道,如何设计空地的长与宽,使所用空地的面积最小?
某校计划在一块空地上建造一个面积为1800m2的矩形游泳池(如图所示),它的两边都留有宽6m的休息台,顶部和底部都留有宽为3m的人行道,如何设计空地的长与宽,使所用空地的面积最小?