题目内容
9.已知圆的方程为(x-1)2+(y+1)2=4,求过圆外一点P(3,2)的切线方程.分析 由题意画出图形,分切线斜率存在和不存在求解,当切线斜率存在时,由圆心到切线的距离等于圆的半径求解.
解答 解:如图,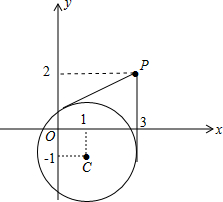
由图可知,过点P(3,2)的圆的切线斜率一条存在,一条不存在,
当切线斜率不存在时,切线方程为x=3;
当切线斜率存在时,设切线方程为y-2=k(x-3),化为一般式:kx-y-3k+2=0.
则圆心C(1,-1)到切线的距离等于半径2,
即$\frac{|k+1-3k+2|}{\sqrt{{k}^{2}+1}}=2$,解得:k=$\frac{5}{12}$.
切线方程为$\frac{5}{12}x-y-\frac{15}{12}+2=0$,即5x-12y+9=0.
故所求圆的切线方程为:x=3或5x-12y+9=0.
点评 本题考查了圆的切线方程的求法,训练了点到直线的距离公式的应用,考查了数形结合的解题思想方法,斜率不存在的切线容易漏掉,是中档题也是易错题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
14.已知集合A={(x,y)|y2=4x},B={(x,y)|y=x+1},则A∩B=( )
| A. | {(1,-2)} | B. | {(1,2)} | C. | (1,2) | D. | (1,-2) |
18.已知函数f(x)=tan(2x-$\frac{π}{3}$),则下列说法错误的是( )
| A. | 函数f(x)的周期为$\frac{π}{2}$ | |
| B. | 函数f(x)的值域为R | |
| C. | 点($\frac{π}{6}$,0)是函数f(x)的图象一个对称中心 | |
| D. | f($\frac{2π}{5}$)<f($\frac{3π}{5}$) |


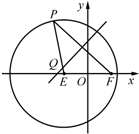 如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
如图,已知圆E:${(x+\sqrt{3})^2}+{y^2}$=16,点$F(\sqrt{3},0)$,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.