题目内容
【题目】已知抛物线E：y2＝2px（p＞0）的焦点为F，以F为圆心，3p为半径的圆交抛物线E于P，Q两点，以线段PF为直径的圆经过点（0，﹣1），则点F到直线PQ的距离为_____．
【答案】
【解析】
由题意设以F为圆心，3p为半径的圆的方程与抛物线联立求出P，Q的坐标，再由以线段PF为直径的圆经过点D（0，﹣1）可得
0，求出p的值，进而求出F的坐标及直线PQ的方程，求出F到直线PQ的距离．
由题意可得以F为圆心，3p为半径的圆的方程为：（x
）2+y2＝（3p）2，
与抛物线方程联立，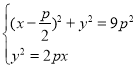
，整理可得4x2+4px﹣35
＝0，所以可得x
，代入抛物线的方程可得y＝±
p，
不妨设P（
，
p），Q（，p），所以直线PQ为x，
因为以线段PF为直径的圆经过点D（0，﹣1），所以0，
即（
，1）（，p+1）＝0，
整理可得：5p2﹣4p+4＝0，所以p
，
所以F（
，0），直线PQ的方程为：x
，
所以点F到直线PQ的距离为
．
故答案为：
练习册系列答案
相关题目
【题目】某商场在促销期间规定：商场内所有商品按标价的
出售，当顾客在商场内消费一定金额后，按如下方案获得相应金额的奖券：
消费金额（元）的范围 |
|
|
|
| … |
获得奖券的金额（元） | 30 | 60 | 100 | 130 | … |
根据上述促销方法，顾客在该商场购物可以获得双重优惠，例如：购买标价为400元的商品，则消费金额为320元，获得的优惠额为：
元，设购买商品得到的优惠率＝（购买商品获得的优惠额）/（商品标价），试问：
（1）若购买一件标价为1000元的商品，顾客得到的优惠率是多少？
（2）对于标价在
（元）内的商品，顾客购买标价为多少元的商品，可得到不小于
的优惠率？
