题目内容
【题目】已知函数f(x)=|x+1|﹣|2x﹣2|的最大值为M,正实数a,b满足a+b=M.
(1)求2a2+b2的最小值;
(2)求证:aabb≥ab.
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】
(1)去绝对值得分段函数: ,由单调性易求函数f(x)的最大值,即有M的值,再由柯西不等式,即可得到所求最小值;
,由单调性易求函数f(x)的最大值,即有M的值,再由柯西不等式,即可得到所求最小值;
(2)应用分析法证明,考虑两边取自然对数,结合因式分解和不等式的性质、对数的性质,即可得证.
解:(1)函数 ,
,
∴![]() 在(∞,1)上单调递增,在(1,+∞)上单调递减,
在(∞,1)上单调递增,在(1,+∞)上单调递减,
当x=1时,f(x)取得最大值![]() ,
,
即M=2,
正实数a,b满足a+b=2,
由柯西不等式可得(2a2+b2)(![]() 1)≥(
1)≥(![]() a
a![]() b)2,
b)2,
化为2a2+b2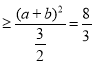 ,
,
所以当![]() ,即b
,即b![]() ,a
,a![]() 时,2a2+b2取得最小值
时,2a2+b2取得最小值![]() ;
;
(2)证明:因为a+b=2,a,b>0,要证aabb≥ab,即证alna+blnb≥lna+lnb,
即证(a﹣1)lna≥(1﹣b)lnb,
即证(a﹣1)lna≥(a﹣1)ln(2﹣a),
即证(1﹣a)ln(![]() 1)≥0,
1)≥0,
当0<a<1时,![]() 1>1,所以ln(
1>1,所以ln(![]() 1)>0,
1)>0,
由1﹣a>0,可得(1﹣a)ln(![]() 1)>0;
1)>0;
当a=1![]() 1)=0;
1)=0;
当1<a<2时,0![]() 1<1,所以ln(
1<1,所以ln(![]() 1)<0,
1)<0,
因为1﹣a<0,所以(1﹣a)ln(![]() 1)>0,
1)>0,
综上所述,(1﹣a)ln(![]() 1)≥0成立,即aabb≥ab.
1)≥0成立,即aabb≥ab.

练习册系列答案
相关题目