题目内容
【题目】设集合A={x|0≤x≤2},B={y|1≤y≤2},在下图中能表示从集合A到集合B的映射的是( )
A.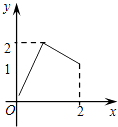
B.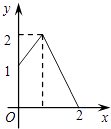
C.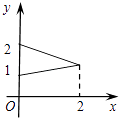
D.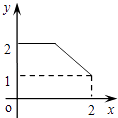
【答案】D
【解析】解:在A中,当0<x<1时,y<1,所以集合A到集合B不成映射,故A不成立;
在B中,1≤x≤2时,y<1,所以集合A到集合B不成映射,故B不成立;
在C中,0≤x≤1时,任取一个x值,在0≤y≤2内,有两个y值与之相对应,所以构不成映射,故C不成立;
在D中,0≤x≤1时,任取一个x值,在0≤y≤2内,总有唯一确定的一个y值与之相对应,故D成立.
故选:D
【考点精析】根据题目的已知条件,利用映射的相关定义的相关知识可以得到问题的答案,需要掌握对于映射f:A→B来说,则应满足:(1)集合A中的每一个元素,在集合B中都有象,并且象是唯一的;(2)集合A中不同的元素,在集合B中对应的象可以是同一个;(3)不要求集合B中的每一个元素在集合A中都有原象;注意:映射是针对自然界中的所有事物而言的,而函数仅仅是针对数字来说的.所以函数是映射,而映射不一定的函数.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此做了四次实验,得到的数据如表:
零件的个数x(个) | 2 | 3 | 4 | 5 |
加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(1)在给定的坐标系中画出表中数据的散点图;
(2)求出y关于x的线性回归方程y= ![]() x+
x+ ![]() ,并在坐标系中画出回归直线;
,并在坐标系中画出回归直线;
(3)试预测加工6个零件需要多少时间?
(注: ![]() =
= 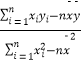 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() )
)