题目内容
选修4-4:坐标系与参数方程
在直角坐标系xoy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sinθ,ρcos(θ-
)=2
.
(Ⅰ)求C1与C2交点的极坐标;
(Ⅱ)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为
(t∈R为参数),求a,b的值.
在直角坐标系xoy中以O为极点,x轴正半轴为极轴建立坐标系.圆C1,直线C2的极坐标方程分别为ρ=4sinθ,ρcos(θ-
| π |
| 4 |
| 2 |
(Ⅰ)求C1与C2交点的极坐标;
(Ⅱ)设P为C1的圆心,Q为C1与C2交点连线的中点,已知直线PQ的参数方程为
|
(I)圆C1,直线C2的直角坐标方程分别为x2+(y-2)2=4,x+y-4=0,
解
得
或
,
∴C1与C2交点的极坐标为(4,
).(2
,
).
(II)由(I)得,P与Q点的坐标分别为(0,2),(1,3),
故直线PQ的直角坐标方程为x-y+2=0,
由参数方程可得y=
x-
+1,
∴
,
解得a=-1,b=2.
解
|
|
|
∴C1与C2交点的极坐标为(4,
| π |
| 2 |
| 2 |
| π |
| 4 |
(II)由(I)得,P与Q点的坐标分别为(0,2),(1,3),
故直线PQ的直角坐标方程为x-y+2=0,
由参数方程可得y=
| b |
| 2 |
| ab |
| 2 |
∴
|
解得a=-1,b=2.

练习册系列答案
相关题目
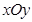 中,已知曲线
中,已知曲线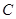 的参数方程是
的参数方程是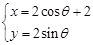 (
(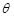 是参数),若以
是参数),若以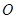 为极点,
为极点,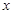 轴的正半轴为极轴,则曲线
轴的正半轴为极轴,则曲线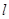 的方程为
的方程为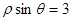 ,则点M
,则点M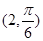 到直线
到直线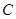 的参数方程为
的参数方程为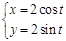 (
(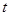 为参数),曲线
为参数),曲线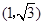 处的切线为
处的切线为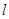 .以坐标原点为极点,
.以坐标原点为极点,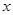 轴的正半轴为极轴建立极坐标系,求
轴的正半轴为极轴建立极坐标系,求 相交于点A、B,则|AB|= 。
相交于点A、B,则|AB|= 。