题目内容
平面直角坐标系中,直线l的参数方程是
(t为参数),以坐标原点为极点,x轴的正半轴为极轴,建立极坐标系,已知曲线C的极坐标方程为ρ2cos2θ+ρ2sin2θ-2ρsinθ-3=0.
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A、B两点,求|AB|.
|
(1)求直线l的极坐标方程;
(2)若直线l与曲线C相交于A、B两点,求|AB|.
(1)直线l的参数方程是
(t为参数),化为普通方程得:y=
x
∴在平面直角坐标系中,直线l经过坐标原点,倾斜角是
,
因此,直线l的极坐标方程是θ=
,(ρ∈R);…(5分)
(2)把θ=
代入曲线C的极坐标方程ρ2cos2θ+ρ2sin2θ-2ρsinθ-3=0,得ρ2-
ρ-3=0
∴由一元二次方程根与系数的关系,得ρ1+ρ2=
,ρ1ρ2=-3,
∴|AB|=|ρ1-ρ2|=
=
.…(10分)
|
| 3 |
∴在平面直角坐标系中,直线l经过坐标原点,倾斜角是
| π |
| 3 |
因此,直线l的极坐标方程是θ=
| π |
| 3 |
(2)把θ=
| π |
| 3 |
| 3 |
∴由一元二次方程根与系数的关系,得ρ1+ρ2=
| 3 |
∴|AB|=|ρ1-ρ2|=
| (ρ1+ρ2)2-4ρ1ρ2 |
| 15 |

练习册系列答案
相关题目
 ,求:
,求: 中
中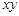 的最大值和最小值.
的最大值和最小值.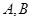 的极坐标为
的极坐标为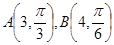 ,则
,则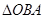 (其中
(其中 为极点)的面积为 .
为极点)的面积为 .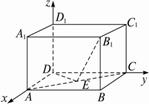
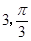 ),(
),(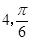 ),则△AOB(其中O为极点)的面积为 .
),则△AOB(其中O为极点)的面积为 .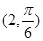 到直线
到直线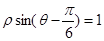 的距离是_______.
的距离是_______.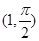 ,且过极点的圆的方程是____________.
,且过极点的圆的方程是____________.