题目内容
2.一个几何体的三视图如图所示,则其体积为( )
| A. | $\frac{4}{3}$(π+1) | B. | $\frac{2}{3}$(π+1) | C. | $\frac{4}{3}$(π+$\frac{1}{2}$) | D. | $\frac{2}{3}$(π+$\frac{1}{2}$) |
分析 由三视图可知,该几何体为组合体,上部为半球,半径为1;下部为正四棱锥,底面正方形的边长为$\sqrt{2}$,高为1;从而求体积.
解答 解:由三视图可知,
该几何体为组合体,上部为半球,半径为1;
下部为正四棱锥,底面正方形的边长为$\sqrt{2}$,高为1;
故其体积V=$\frac{1}{2}$×$\frac{4}{3}$×π×13+$\frac{1}{3}$×$(\sqrt{2})^{2}$×1=$\frac{2}{3}$(π+1);
故选B.
点评 本题考查了学生的空间想象力及计算能力,属于基础题.

练习册系列答案
相关题目
12.若复数z满足(3-4i)z=|4+3i|,则z的虚部为( )
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$i | C. | $\frac{4}{5}$i | D. | 4 |
13.已知函数f(x)是定义在R上的偶函数,且在区间[0,+∞)上是减函数,若$f({ln\frac{n}{m}})-f(1)>0$,则$\frac{{{m^2}+{n^2}}}{mn}$的取值范围是( )
| A. | [2,+∞) | B. | [2,e) | C. | $({e+\frac{1}{e},+∞})$ | D. | $[{2,e+\frac{1}{e}})$ |
10.i为虚数单位,(1+i)$\overline{z}$=(1-i)2,则|z|=( )
| A. | 1 | B. | 2 | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
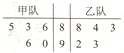 某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示:
某项比赛规则是:先进行个人赛,每支参赛队的成绩前三名队员再代表本队进行团体赛,团体赛是在两队名次相同队员之间进行且三场比赛同时进行.根据以往比赛统计:两名队员中个人赛成绩高的队员在各场获胜的概率为$\frac{2}{3}$,负的概率为$\frac{1}{3}$,且各场比赛互不影响.已知甲乙队各5名队员,这10名队员的个人赛成绩如图所示: