题目内容
【题目】(本小题共13分)已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,a2=4, S5=35.
,a2=4, S5=35.
(Ⅰ)求数列![]() 的前
的前![]() 项和
项和![]() ;
;
(Ⅱ)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的前n项和
的前n项和![]() .
.
【答案】解:(Ⅰ)设数列![]() 的首项为a1,公差为d.
的首项为a1,公差为d.
则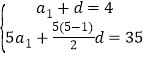 ∴
∴![]() , ………………5分
, ………………5分
∴![]() .
.
∴ 前![]() 项和
项和![]() . ……………7分
. ……………7分
(Ⅱ)∵![]() ,
,
∴![]() ,且b1=e. ………………8分
,且b1=e. ………………8分
当n≥2时,
![]() 为定值, ………………10分
为定值, ………………10分
∴ 数列![]() 构成首项为e,公比为e3的等比数列. ……………11分
构成首项为e,公比为e3的等比数列. ……………11分
∴![]() . ………………13分
. ………………13分
数列![]() 的前n项的和是
的前n项的和是![]() .
.
【解析】
l
试题(Ⅰ)由题可知,根据等差数列的通项公式以及前n项和公式,可解得![]() ,所以前n项和为
,所以前n项和为![]() ;(Ⅱ)由(Ⅰ)可得,
;(Ⅱ)由(Ⅰ)可得,![]() ,当
,当![]() 时,
时,![]() ,可知其是首项为e,公比为e3的等比数列,故
,可知其是首项为e,公比为e3的等比数列,故![]() ;
;
试题解析:(Ⅰ)设数列![]() 的首项为a1,公差为d.
的首项为a1,公差为d.
则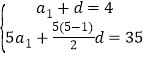 ∴
∴![]() ,
,
所以![]() .
.
故前![]() 项和
项和![]() .
.
(Ⅱ)由于![]() ,故
,故![]() ,且b1=e.
,且b1=e.
当n≥2时,![]() 为定值,
为定值,
所以数列![]() 构成首项为e,公比为e3的等比数列.
构成首项为e,公比为e3的等比数列.
故![]() .
.
数列![]() 的前n项的和是
的前n项的和是![]() .
.

练习册系列答案
相关题目