题目内容
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
(1)求曲线C1的一般方程和曲线C2的直角坐标方程;
(2)若点P在曲线C1上,点Q曲线C2上,求|PQ|的最小值.
【答案】(1)![]() ,(x﹣2)2+y2=1;(2)2.
,(x﹣2)2+y2=1;(2)2.
【解析】
(1)由C1的参数方程为![]() 为参数),消去参数即可转换为直角坐标方程,根据曲线C2:ρ2﹣4ρcosθ+3=0.利用
为参数),消去参数即可转换为直角坐标方程,根据曲线C2:ρ2﹣4ρcosθ+3=0.利用![]() 转换为直角坐标方程.
转换为直角坐标方程.
(2)设点P(5cosθ,4sinθ),根据点Q在圆上,先求点P到圆心的距离,然后减去半径即为最小值.
(1)曲线C1的参数方程为![]() 为参数),
为参数),
两式平方相加整理得![]() .
.
将![]() 代入ρ2﹣4ρcosθ+3=0.
代入ρ2﹣4ρcosθ+3=0.
得x2+y2﹣4x+3=0,
整理得(x﹣2)2+y2=1.
(2)设点P(5cosθ,4sinθ)在曲线C1上,圆心O(2,0),
所以: ,
,
当cosθ=1时,|PO|min=3,
所以|PQ|的最小值3﹣1=2.

练习册系列答案
相关题目
【题目】在某市高中某学科竞赛中,某一个区4000名考生的参赛成绩统计如图所示.
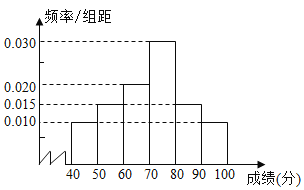
(1)求这4000名考生的竞赛平均成绩![]() (同一组中数据用该组区间中点作代表);
(同一组中数据用该组区间中点作代表);
(2)记70分以上为优秀,70分及以下为合格,结合频率分布直方图完成下表,并判断是否有99%的把握认为该学科竞赛成绩与性别有关?
合格 | 优秀 | 合计 | |
男生 | 720 |
|
|
女生 |
| 1020 |
|
合计 |
|
| 4000 |
附:
p(k2≥k0) | 0.010 | 0.005 | 0.001 |
k0 | 6.635 | 7.879 | 10.828 |
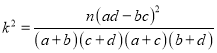 .
.