题目内容
(本题满分14分)
已知椭圆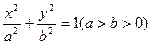 的离心率为
的离心率为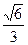 ,长轴长为
,长轴长为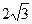 ,直线
,直线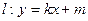 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。
(1)求椭圆的方程;
(2)求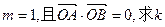 的值(O点为坐标原点);
的值(O点为坐标原点);
(3)若坐标原点O到直线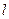 的距离为
的距离为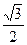 ,求
,求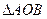 面积的最大值。
面积的最大值。
已知椭圆
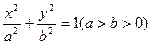 的离心率为
的离心率为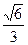 ,长轴长为
,长轴长为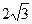 ,直线
,直线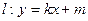 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。(1)求椭圆的方程;
(2)求
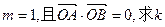 的值(O点为坐标原点);
的值(O点为坐标原点);(3)若坐标原点O到直线
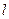 的距离为
的距离为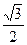 ,求
,求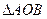 面积的最大值。
面积的最大值。(1)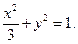 (2)
(2) (3)
(3)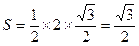
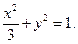 (2)
(2) (3)
(3)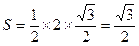
(1)设椭圆的半焦距为c,
依题意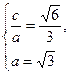
解得
由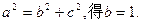 2分
2分
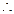 所求椭圆方程为
所求椭圆方程为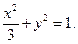 3分
3分
(2)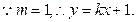
设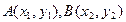 ,
,
其坐标满足方程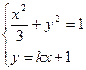
消去 并整理得
并整理得
 4分
4分
则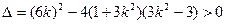 (*) 5分
(*) 5分
故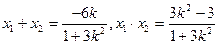 6分
6分

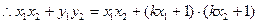
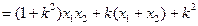
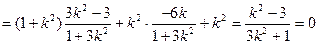

经检验 满足式(*)式 8分
满足式(*)式 8分
(3)由已知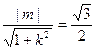 ,
,
可得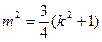 9分
9分
将
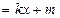 代入椭圆方程,
代入椭圆方程,
整理得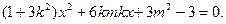
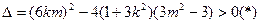
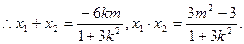 10分
10分
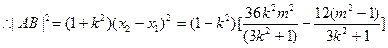
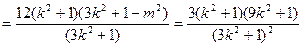 11分
11分
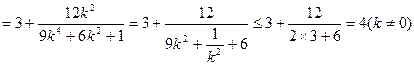 12分
12分
当且仅当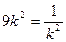 ,
,
即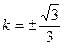 时等号成立,
时等号成立,
经检验,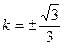 满足(*)式
满足(*)式
当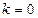 时,
时,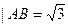
综上可知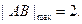 13分
13分
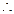 当|AB最大时,
当|AB最大时,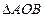 的面积最大值
的面积最大值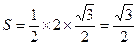 14分
14分
依题意
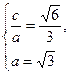
解得

由
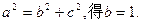 2分
2分 所求椭圆方程为
所求椭圆方程为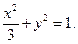 3分
3分(2)
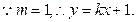
设
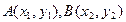 ,
,其坐标满足方程
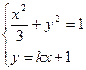
消去
 并整理得
并整理得 4分
4分则
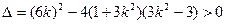 (*) 5分
(*) 5分故
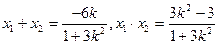 6分
6分
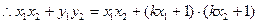
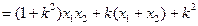
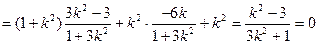

经检验
 满足式(*)式 8分
满足式(*)式 8分(3)由已知
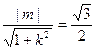 ,
,可得
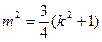 9分
9分将

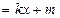 代入椭圆方程,
代入椭圆方程,整理得
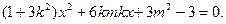
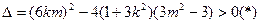
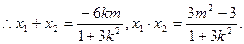 10分
10分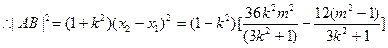
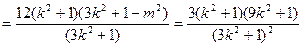 11分
11分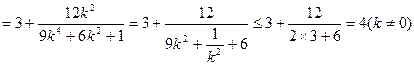 12分
12分当且仅当
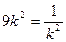 ,
,即
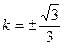 时等号成立,
时等号成立,经检验,
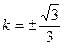 满足(*)式
满足(*)式当
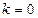 时,
时,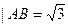
综上可知
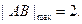 13分
13分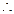 当|AB最大时,
当|AB最大时,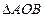 的面积最大值
的面积最大值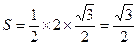 14分
14分
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
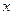 轴上的椭圆经过点M(1,
轴上的椭圆经过点M(1,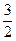 ),斜率为
),斜率为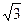 的直线经过椭圆的下顶点D和右焦点F,A、B为椭圆上不同于M的两点。
的直线经过椭圆的下顶点D和右焦点F,A、B为椭圆上不同于M的两点。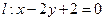 过椭圆的左焦点
过椭圆的左焦点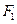 和一个顶点
和一个顶点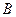 ,该椭圆的离心率为
,该椭圆的离心率为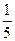
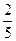
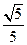
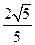
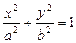 (
(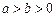 )的离心率为
)的离心率为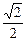 ,且短轴长为2.
,且短轴长为2.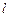 与椭圆交于
与椭圆交于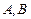 两点,
两点,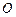 为坐标原点,且
为坐标原点,且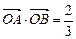 ,
,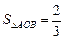 ,求直线
,求直线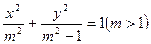 上一点P到其左焦点的距离为3,到右焦点的距离为1,则P点到右准线的距离为
上一点P到其左焦点的距离为3,到右焦点的距离为1,则P点到右准线的距离为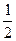
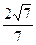
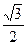 ,与直线x+y-1=0相交于两点M、N,且以
,与直线x+y-1=0相交于两点M、N,且以 为直径的圆经过坐标原点.求椭圆的方程.
为直径的圆经过坐标原点.求椭圆的方程.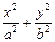 =1(a>b>0)的左、右两个焦点.
=1(a>b>0)的左、右两个焦点.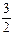 )到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;
)到F1、F2两点的距离之和等于4,写出椭圆C的方程和焦点坐标;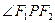 最大,说明理由,并求出最大值。
最大,说明理由,并求出最大值。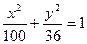 上的点P到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )
上的点P到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )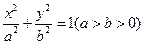 的两个焦点分别为
的两个焦点分别为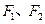 ,点
,点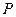 在椭圆上,且
在椭圆上,且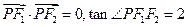 ,则椭圆的离心率等于 .
,则椭圆的离心率等于 .