题目内容
已知定义域是（0，+∞）的函数f（x）满足；
（1）对任意x∈（0，+∞），恒有f（3x）=3f（x）成立；
（2）当x∈（1，3]时，f（x）=3-x．给出下列结论：
①对任意m∈Z，有f（3m）=0；
②函数f（x）的值域为[0，+∞）；
③存在n∈Z，使得f（3n+1）=0；
④“函数f（x）在区间（a，b）上单调递减”的充要条件是“?k∈Z，使得（a，b）⊆（3k，3k+1）．”
其中正确结论的序号是______．
（1）对任意x∈（0，+∞），恒有f（3x）=3f（x）成立；
（2）当x∈（1，3]时，f（x）=3-x．给出下列结论：
①对任意m∈Z，有f（3m）=0；
②函数f（x）的值域为[0，+∞）；
③存在n∈Z，使得f（3n+1）=0；
④“函数f（x）在区间（a，b）上单调递减”的充要条件是“?k∈Z，使得（a，b）⊆（3k，3k+1）．”
其中正确结论的序号是______．
①∵对任意x∈（0，+∞），恒有f（3x）=3f（x）成立，当x∈（1，3]时，f（x）=3-x．
∴f（3m）=f（3•3m-1）=3f（3m-1）=…=3m-1f（3）=0，故①正确；
②取x∈（3m，3m+1]，则
∈（1，3]，
f（
）=3-
，f（
）=…=3mf（
）=3m+1-x，从而函数f（x）的值域为[0，+∞）；即②正确；=3m+1-x，
从而f（x）∈[0，+∞），故②正确；
③∵x∈（1，3]时，f（x）=3-x，对任意x∈（0，+∞），恒有f（3x）=3f（x）成立，n∈Z，
∴f（3n+1）=3nf（1+
）=3n[3-（1+
）]=3n（2-
）≠0，故③错误；
④令3k≤a＜b≤3k+1，
则1≤
＜
≤3，
∴f（a）-f（b）=f（3k•
）-f（3k•
）=3k[f（
）-f（
）]=3k[（3-
）-（3-
）]=3k（
-
）=b-a＞0，
∴函数f（x）在区间（a，b））⊆（3k，3k+1）上单调递减，
故④正确；
综上所述，正确结论的序号是①②④．
故答案为：①②④．
∴f（3m）=f（3•3m-1）=3f（3m-1）=…=3m-1f（3）=0，故①正确；
②取x∈（3m，3m+1]，则
| x |
| 3m |
f（
| x |
| 3m |
| x |
| 3m |
| x |
| 3 |
| x |
| 3m |
从而f（x）∈[0，+∞），故②正确；
③∵x∈（1，3]时，f（x）=3-x，对任意x∈（0，+∞），恒有f（3x）=3f（x）成立，n∈Z，
∴f（3n+1）=3nf（1+
| 1 |
| 3n |
| 1 |
| 3n |
| 1 |
| 3n |
④令3k≤a＜b≤3k+1，
则1≤
| a |
| 3k |
| b |
| 3k |
∴f（a）-f（b）=f（3k•
| a |
| 3k |
| b |
| 3k |
| a |
| 3k |
| b |
| 3k |
| a |
| 3k |
| b |
| 3k |
| b |
| 3k |
| a |
| 3k |
∴函数f（x）在区间（a，b））⊆（3k，3k+1）上单调递减，
故④正确；
综上所述，正确结论的序号是①②④．
故答案为：①②④．
练习册系列答案
相关题目
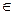R,f(x)=f(x+1)+f(x-1)恒成立.
.
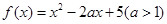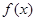的定义域和值域均是
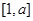，求实数
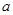的值；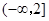
上是减函数，且对任意的
，
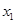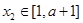，总有
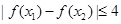，求实数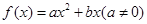
满足条件：①
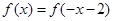；②函数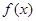
的图像与直线
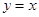相切．
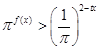在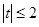
时恒成立，求实数
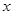的取值范围．
