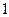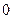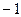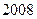题目内容
已知f(x)是实数集R上的函数,且对任意x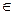 R,f(x)=f(x+1)+f(x-1)恒成立.
R,f(x)=f(x+1)+f(x-1)恒成立.
(1)求证:f(x)是周期函数.
(2)已知f(3)=2,求f(2 004).
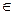 R,f(x)=f(x+1)+f(x-1)恒成立.
R,f(x)=f(x+1)+f(x-1)恒成立.(1)求证:f(x)是周期函数.
(2)已知f(3)=2,求f(2 004).
(1)证明见解析(2)-2
(1)证明 ∵f(x)=f(x+1)+f(x-1),∴f(x+1)=f(x)-f(x-1),
则f(x+2)=f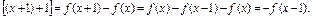
∴f(x+3)=f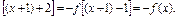
∴f(x+6)=f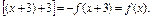
∴f(x)是周期函数且6是它的一个周期.
(2)解 f(2 004)=f(334×6)=f(0)=-f(3)=-2.
则f(x+2)=f
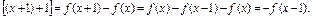
∴f(x+3)=f
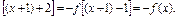
∴f(x+6)=f
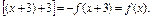
∴f(x)是周期函数且6是它的一个周期.
(2)解 f(2 004)=f(334×6)=f(0)=-f(3)=-2.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
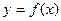 ,
,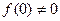 ,当
,当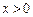 时,
时,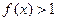 ,且
,且 ∈R,有
∈R,有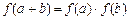 .
. ;
;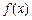 是R上的增函数;
是R上的增函数;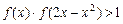 ,求
,求 的取值范围.
的取值范围.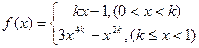 满足
满足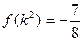 ;
;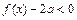 恒成立,求a的取值范围.
恒成立,求a的取值范围.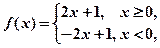 则f(-2)= 、已知
则f(-2)= 、已知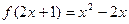 ,则
,则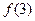 = ;.
= ;.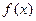 满足
满足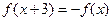 ,当
,当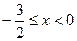 时,
时,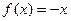 ,
,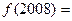 ( )
( )