题目内容
14.化简:(1)$\overrightarrow{AB}$-$\overrightarrow{AC}$+$\overrightarrow{BD}$-$\overrightarrow{CD}$;
(2)$\overrightarrow{AB}$+$\overrightarrow{MB}$+$\overrightarrow{BO}$+$\overrightarrow{OM}$;
(3)$\overrightarrow{MB}$+$\overrightarrow{AC}$+$\overrightarrow{BM}$;
(4)$\overrightarrow{OA}$+$\overrightarrow{OC}$+$\overrightarrow{BO}$+$\overrightarrow{CO}$.
分析 根据向量加法、减法的几何意义,用有向线段的起点和终点表示向量,以及相反向量的概念进行向量的加法和减法的运算从而化简每个式子即可.
解答 解:(1)$\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BD}-\overrightarrow{CD}=\overrightarrow{CB}+\overrightarrow{BD}+\overrightarrow{DC}$=$\overrightarrow{0}$;
(2)$\overrightarrow{AB}+\overrightarrow{MB}+\overrightarrow{BO}+\overrightarrow{OM}$=$\overrightarrow{AB}+\overrightarrow{MB}+\overrightarrow{BM}=\overrightarrow{AB}$;
(3)$\overrightarrow{MB}+\overrightarrow{AC}+\overrightarrow{BM}=\overrightarrow{MB}+\overrightarrow{BM}+\overrightarrow{AC}$=$\overrightarrow{AC}$;
(4)$\overrightarrow{OA}+\overrightarrow{OC}+\overrightarrow{BO}+\overrightarrow{CO}=\overrightarrow{BO}+\overrightarrow{OA}$$+\overrightarrow{OC}+\overrightarrow{CO}=\overrightarrow{MA}+\overrightarrow{0}=\overrightarrow{MA}$
点评 考查向量、向量加法,以及向量减法的几何意义,相反向量和零向量的概念.

| A. | (1,2015) | B. | (1,2016) | C. | (2,2016) | D. | [2,2016] |
| A. | R | B. | {x|x∈R,x≠0} | C. | {0} | D. | ∅ |
| A. | 不存在x∈R,x3-1≤0 | B. | 存在x∈R,x3-1≤0 | ||
| C. | 存在x∈R.x3-1>0 | D. | 对任意的x∈R,x3-1>0 |
| A. | ${a_n}={(\frac{3}{2})^{n-1}}$ | B. | ${a_n}=3×{(\frac{1}{2})^{n-1}}$ | C. | an=3n-2 | D. | ${a_n}={3^{n-1}}$ |
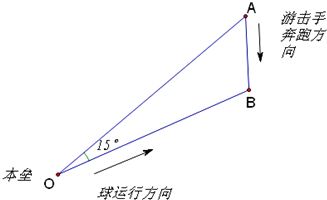 在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)
在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)