题目内容
4.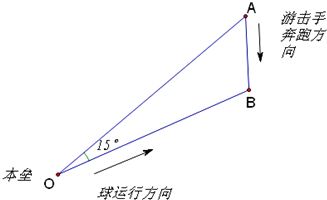 在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)
在奥运会垒球比赛前,C国教练布置战术时,要求击球手以与连结本垒及游击手的直线成15°的方向把球击出,根据经验及测速仪的显示,通常情况下球速为游击手最大跑速的4倍,问按这样的布置,游击手能不能接着球?(如图所示)
分析 先假设能够接到球且接球点为B,设游击手从点A跑出,本垒为O点构造三角形OAB,再假设从击出球到接着球的时间为t,球速为v,在三角形POAB中可得到OB=vt,AB≤$\frac{y}{4}$•t,然后根据正弦定理可得到sin∠OAB的值,结果发现sin∠OAB>1不成立,故接不到球.
解答 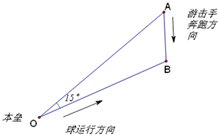 解:如图,设游击手能接着球,接球点为B,而游击手从点A跑出,本垒为O点.
解:如图,设游击手能接着球,接球点为B,而游击手从点A跑出,本垒为O点.
设从击出球到接着球的时间为t,球速为v,则∠AOB=15°,
OB=vt,AB≤$\frac{y}{4}$•t.
在△AOB中,由正弦定理,得$\frac{OB}{sin∠OAB}=\frac{AB}{sin15°}$,
sin∠OAB=$\frac{OBsin15°}{AB}$≥$\frac{\sqrt{6}-\sqrt{2}}{4}•\frac{4vt}{vt}$=$\sqrt{6}$-$\sqrt{2}$,
而($\sqrt{6}$-$\sqrt{2}$)2=8-4$\sqrt{3}$>8-4×1.74>1,
即sin∠OAB>1,
∴这样的∠OAB不存在,因此游击手不能接着球.
点评 本题主要考查正弦定理在现实生活中的应用.考查考生的对问题的理解和认识的深度.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
15.在(a+b)n中展开式中第7项二项式系数最大,则n=( )
| A. | 12 | B. | 11或13 | C. | 11或12或13 | D. | 12或13 |
19.若框图所给的程序运行结果为S=1,那么判断框中应填入的关于k的条件可以是( )
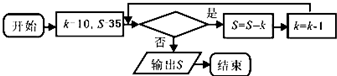

| A. | k=7 | B. | k≤6 | C. | k<6 | D. | k>6 |