题目内容
4. 如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点.在此几何体中,给出下面四个结论:
如图是一几何体的平面展开图,其中ABCD为正方形,E,F分别为PA,PD的中点.在此几何体中,给出下面四个结论:①B,E,F,C四点共面;
②直线BF与AE异面;
③直线EF∥平面PBC;
④平面BCE⊥平面PAD;.
⑤折线B→E→F→C是从B点出发,绕过三角形PAD面,到达点C的一条最短路径.
其中正确的有①②③.(请写出所有符合条件的序号)
分析 首先可根据几何体的平面展开图画出其直观图,然后根据中位线的性质,两条平行直线可确定一个平面,异面直线的概念,线面平行的判定定理,二面角的平面角的定义及求法,即可判断每个结论的正误,而对于结论⑤,可画出该几何体沿底面正方形的边,及侧棱PD剪开后所得的平面展开图,由该展开图即可求出从B点出发,绕过平面PAD,到达点C的最短距离,从而判断出该结论的正误.
解答 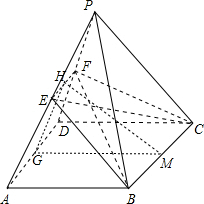 解:根据几何体的平面展开图,画出它的直观图如下:
解:根据几何体的平面展开图,画出它的直观图如下:
①根据已知,EF∥AD∥BC;
∴EF∥BC;
∴B,E,F,C四点共面;
∴该结论正确;
②由图可看出BF和AE异面;
∴该结论正确;
③由①EF∥BC,EF?平面PBC,BC?平面PBC;
∴EF∥平面PBC;
∴该结论正确;
④分别取AD,EF,BC的中点G,H,M,并连接GH,HM,MG,则GH⊥EF,HM⊥EF;
而EF是平面BCE和平面PAD的交线;
∴∠GHM为平面BCE与平面PAD形成的二面角的平面角;
若设该几何体的侧棱长为2,则:
GH=$\frac{\sqrt{3}}{2}$,HM=$\frac{\sqrt{11}}{2}$,MG=2;
显然GH2+HM2≠MG2;
∴∠GHM≠90°;
∴平面BCE与平面PAD不垂直;
∴该结论错误;
⑤把该正四棱锥沿底面各边及侧棱PD剪开,得到的展开图如下: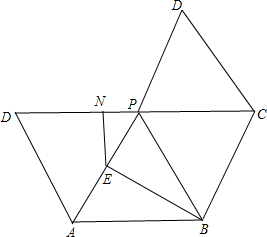
BH⊥PA,∴B到侧棱PA的最短距离为BE,BE=$\sqrt{3}$;
过E作EN⊥PD,则EN是点E到PD的最短距离,且EN=$\frac{\sqrt{3}}{2}$,NP=$\frac{1}{4}$;
而N到C的最短距离便是线段NC的长,NC=$\frac{9}{4}$;
∴从B点出发,绕过PAD面到达C点的最短距离为$\sqrt{3}+\frac{\sqrt{3}}{2}+\frac{9}{4}=\frac{3\sqrt{3}}{2}+\frac{9}{4}$;
而BE+EF+FC=$2\sqrt{3}+1$;
∴该结论错误;
综上得正确的结论为①②③.
故答案为:①②③.
点评 考查中位线的性质,两平行直线可确定一个平面,能根据几何体的平面展开图画出它的直观图,线面平行的判定定理,以及二面角的平面角的概念及求法,将立体图形转变成平面图形解题的方法.


| A. | a>b | B. | a<b | ||
| C. | a=b | D. | a,b的大小关系不能确定 |
| A. | a<b<c<d | B. | b<a<c<d | C. | c<d<a<b | D. | c<d<b<a |
