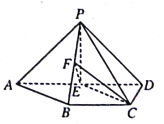
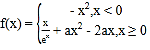题目内容
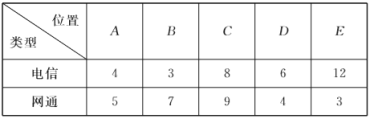
【题目】现有10件产品中有3件次品,7件正品,从中抽取5件![]() 用数字表示
用数字表示![]()
(1)没有次品的抽法有多少种?
(2)有2件次品的抽法有多少种?
(3)至少1件次品的抽法有多少种?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)没有次品即全为正品,利用组合数公式计算可得;
(2)事件分两步完成,第一步从3件次品中抽取2件次品,第二步从7件正品中抽取3件正品,根据乘法原理计算求得,
(3)事件至少抽出1件次品包括抽取1件次品,抽取2件次品和抽取3件次品三类,利用乘法原理分别计算三类的得数,再利用加法原理计算求得.
解:(1)![]() 共10件产品中有3件次品,从中任意抽出5件产品,没有次品的抽法有
共10件产品中有3件次品,从中任意抽出5件产品,没有次品的抽法有![]() 种;
种;
(2)![]() 共10件产品中有3件次品,从中任意抽出5件产品,
共10件产品中有3件次品,从中任意抽出5件产品,
![]() 其中恰好抽出2件次品的抽法有
其中恰好抽出2件次品的抽法有![]() 种,
种,
(3)从10件产品中,任意抽取5件产品,
其中至少抽出1件次品包括抽取1件次品,抽取2件次品和抽取3件次品三类
故至少抽出1件次品的抽法有![]() 种.
种.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】在2016年8月巴西里约热内卢举办的第31届奥运会上,乒乓球比赛团体决赛实行五场三胜制,且任何一方获胜三场比赛即结束.甲、乙两个代表队最终进入决赛,根据双方排定的出场顺序及以往战绩统计分析,甲队依次派出的五位选手分别战胜对手的概率如下表:
出场顺序 | 1号 | 2号 | 3号 | 4号 | 5号 |
获胜概率 |
|
|
|
|
|
若甲队横扫对手获胜(即3∶0获胜)的概率是![]() ,比赛至少打满4场的概率为
,比赛至少打满4场的概率为![]() .
.
(1)求![]() ,
,![]() 的值;
的值;
(2)求甲队获胜场数的分布列和数学期望.