��Ŀ����
����Ŀ������һ���ڼ䣬���������̳��ֱ�չ�����.
�����̳��Ĺ����ǣ���������100Ԫ���ɳ齱һ�Σ���װ�д�С����״��ͬ��4������4������Ĵ�������4�����н�������±���
�����Ľ�� | ��ý��𣨵�λ��Ԫ�� |
4�������4������ | 200 |
3������1�������3������1������ | 20 |
2������2������ | 10 |
��![]() Ϊ�齱һ�λ�õĽ�����
Ϊ�齱һ�λ�õĽ�����![]() �ķֲ��к�����.
�ķֲ��к�����.
�������̳��Ĺ����ǣ���������100Ԫ���ɳ齱10��.���У���![]() �γ齱�����ǣ��ӱ��Ϊ
�γ齱�����ǣ��ӱ��Ϊ![]() �Ĵ��У�װ�д�С����״��ͬ��
�Ĵ��У�װ�д�С����״��ͬ��![]() �������
�������![]() ����������
����������![]() ������������
�������ô�������![]() ������ɫ����ͬ����ɻ�ý���
������ɫ����ͬ����ɻ�ý���![]() Ԫ���ǵ�
Ԫ���ǵ�![]() �λ���
�λ���![]() .����������Ľ������Ӱ�죬��������õ��ܽ���Ϊ10�ν���֮��.
.����������Ľ������Ӱ�죬��������õ��ܽ���Ϊ10�ν���֮��.
����֤��![]() ��
��
����ij�˿���120Ԫ����Ʒ���������������أ��ӻ�ý����������������Ӧ��ѡ����һ���̳���
���𰸡����ֲ��м�����������Ϊ20����������֤������������ѡ����̳�.
��������
������![]() �����п�����ֵΪΪ200��20��10���ֱ�������ʣ��ɴ������
�����п�����ֵΪΪ200��20��10���ֱ�������ʣ��ɴ������![]() �ķֲ��к�������
�ķֲ��к�������
����������![]() ��2��3��
��2��3��![]() ��
��![]() ��
Ϊ��![]() �γ齱��õĽ���
�γ齱��õĽ���![]() ��ȡֵΪ
��ȡֵΪ![]() ��0�����
��0�����![]() ����֤��
����֤��![]() ������
������![]() �����ڼ��̳��齱�ý��������ֵ���ߣ���ѡ���̳���
�����ڼ��̳��齱�ý��������ֵ���ߣ���ѡ���̳���
������![]() �����п�����ֵΪΪ200��20��10��
�����п�����ֵΪΪ200��20��10��
![]() ��
��
![]() ��
��
![]() ��
��
![]() ��
��
����������![]() ��2��3��
��2��3��![]() ��
��![]() ��
Ϊ��![]() �γ齱��õĽ���
�γ齱��õĽ���![]() ��ȡֵΪ
��ȡֵΪ![]() ��0��
��0��
��![]() ��
��
��![]() ��
��
����![]()
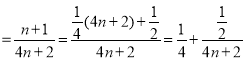 .
.
����![]() �ڶ������ڵ����ݼ�������
�ڶ������ڵ����ݼ�������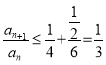 .
.
����![]() ��
��
�������![]() ��
��![]() ��2��3��
��2��3��![]() ��10��
��10��
��![]() Ϊ�����̳��齱��õ��ܽ�����
Ϊ�����̳��齱��õ��ܽ�����![]() ��
��
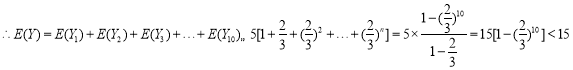
![]() �����ڼ��̳��齱�ý��������ֵ���ߣ���ѡ���̳���
�����ڼ��̳��齱�ý��������ֵ���ߣ���ѡ���̳���

 ��ɢ˼ά�¿���ϵ�д�
��ɢ˼ά�¿���ϵ�д�