题目内容
2.点F是抛物线τ:x2=2py(p>0)的焦点,F1是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点,若线段FF1的中点P恰为抛物线τ与双曲线C的渐近线在第一象限内的交点,则双曲线C的离心率e的值为( )| A. | $\frac{{3\sqrt{2}}}{2}$ | B. | $\frac{{3\sqrt{3}}}{4}$ | C. | $\frac{9}{8}$ | D. | $\frac{{3\sqrt{2}}}{4}$ |
分析 双曲线C的渐近线方程为y=$\frac{b}{a}$x,代入x2=2py,可得P($\frac{2bp}{a}$,$\frac{2{b}^{2}p}{{a}^{2}}$),利用P是线段FF1的中点,可得P($\frac{c}{2}$,$\frac{p}{4}$),由此即可求出双曲线C的离心率.
解答 解:双曲线C的渐近线方程为y=$\frac{b}{a}$x,代入x2=2py,可得P($\frac{2bp}{a}$,$\frac{2{b}^{2}p}{{a}^{2}}$),
∵F(0,$\frac{p}{2}$),F1(c,0)
∴线段FF1的中点P($\frac{c}{2}$,$\frac{p}{4}$),
∴$\frac{2bp}{a}$=$\frac{c}{2}$,$\frac{2{b}^{2}p}{{a}^{2}}$=$\frac{p}{4}$,
∴a2=8b2,
∴c2=9b2,
∴e=$\frac{c}{a}$=$\frac{3\sqrt{2}}{4}$.
故选:D.
点评 本题考查双曲线C的离心率,考查抛物线、双曲线的性质,考查学生的计算能力,确定P的坐标是关键.

练习册系列答案
相关题目
12.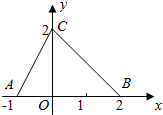 如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )
如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )
 如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )
如图,函数f(x)的图象为折线ACB,则不等式f(x)>2x-1的解集是( )| A. | {x|-1<x≤0} | B. | {x|-1≤x≤1} | C. | {x|-1≤x<1} | D. | {x|-1<x≤2} |
13.圆x2+y2-2x+4y=0与2tx-y-2-2t=0(t∈R)的位置关系为( )
| A. | 相离 | B. | 相切 | C. | 相交 | D. | 以上都有可能 |
7.tan(-330°)的值为( )
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}$ | D. | $\sqrt{3}$ |