题目内容
【题目】如图,在底面是直角梯形的四棱锥S-ABCD中,![]() 面
面![]() .
.

(1)求四棱锥S-ABCD的体积;
(2)求证:面![]()
![]()
(3)求SC与底面ABCD所成角的正切值。
【答案】(1)![]() ;(2)见解析(3)
;(2)见解析(3)![]() .
.
【解析】
(1)根据梯形的面积公式及四棱锥的体积公式直接求值即可.
(2)先由SA⊥面ABCD,可得SA⊥BC,再由AB⊥BC ,得BC⊥平面SAB,从而证得平面SAB⊥平面SBC.
(3)找到线面角是解决问题的关键.连接AC ∵SA⊥面ABCD
∴∠SCA为SC与底面ABCD所成的角,然后解三角形即可.
证明:(1)S梯形ABCD=![]() (AD+BC)·AB=
(AD+BC)·AB=![]() (
(![]() +1)×1=
+1)×1=![]()
VS-ABCD=![]() ×
×![]() ×1=
×1=![]() ……………2分
……………2分
(2)∵SA⊥面ABCD ∴SA⊥BC……………………………………3分
又AB⊥BC ∴BC⊥平面SAB
∴平面SAB⊥平面SBC……………………………………5分
(3)连接AC ∵SA⊥面ABCD
∴∠SCA为SC与底面ABCD所成的角……………………………………7分
在Rt△ABC中,AC=![]() =
=![]()
在Rt△SAC中,tan∠SCA=![]() =
=![]() =
=![]() ……………………………………9分
……………………………………9分

 名校课堂系列答案
名校课堂系列答案【题目】某学校举行了一次安全教育知识竞赛,竞赛的原始成绩采用百分制,已知高三学生的原始成绩均分布在![]() 内,发布成绩使用等级制,各等级划分标准见表.
内,发布成绩使用等级制,各等级划分标准见表.
原始成绩 | 85分及以上 | 70分到84分 | 60分到69分 | 60分以下 |
等级 | 优秀 | 良好 | 及格 | 不及格 |
为了解该校高三年级学生安全教育学习情况,从中抽取了![]() 名学生的原始成绩作为样本进行统计,按照
名学生的原始成绩作为样本进行统计,按照![]() 的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
的分组作出频率分布直方图如图所示,其中等级为不及格的有5人,优秀的有3人.
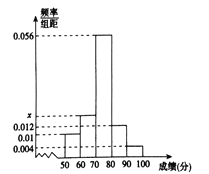
(1)求![]() 和频率分布直方图中的
和频率分布直方图中的![]() 的值;
的值;
(2)根据样本估计总体的思想,以事件发生的频率作为相应事件发生的概率,若该校高三学生共1000人,求竞赛等级在良好及良好以上的人数;
(3)在选取的样本中,从原始成绩在80分以上的学生中随机抽取2名学生进行学习经验介绍,求抽取的2名学生中优秀等级的学生恰好有1人的概率.