题目内容
【题目】用数学归纳法证明“n3＋(n＋1)3＋(n＋2)3 ， (n∈N＋)能被9整除”，要利用归纳法假设证n＝k＋1时的情况，只需展开（ ）．
A.(k＋3)3
B.(k＋2)3
C.(k＋1)3
D.(k＋1)3＋(k＋2)3
【答案】A
【解析】假设n＝k时，原式k3＋(k＋1)3＋(k＋2)3能被9整除，当n＝k＋1时，(k＋1)3.＋(k＋2)3＋(k＋3)3为了能用上面的归纳假设，只须将(k＋3)3展开，让其出现k3即可．故应选A.
【考点精析】通过灵活运用数学归纳法的步骤，掌握
- 步骤:A.命题在n=1（或
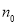）时成立，这是递推的基础；B.假设在n=k时命题成立； C.证明n=k+1时命题也成立,完成这两步,就可以断定对任何自然数(或n>=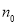,且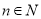
)结论都成立
即可以解答此题．
练习册系列答案
相关题目
