题目内容
【题目】已知f(x)=x2﹣(m+ ![]() )x+1
)x+1
(1)当m=2时,解不等式f(x)≤0
(2)若m>0,解关于x的不等式f(x)≥0.
【答案】
(1)解:m=2时,不等式化为(x﹣ ![]() )(x﹣2)≤0,
)(x﹣2)≤0,
∴ ![]() ,
,
∴不等式的解集为{x| ![]() }
}
(2)解:由题意得f(x)=(x﹣m)(x﹣ ![]() )
)
当0<m<1时,m< ![]() ,不等式解集为{x|x≤m或x≥
,不等式解集为{x|x≤m或x≥ ![]() }
}
当m=1时,m= ![]() ,不等式解集为R
,不等式解集为R
当m>1时,m> ![]() ,不等式解集为{x|x≥m或x≤
,不等式解集为{x|x≥m或x≤ ![]() }
}
【解析】(1)m=2时,不等式化为(x﹣ ![]() )(x﹣2)≤0,即可解不等式f(x)≤0(2)若m>0,分类讨论解关于x的不等式f(x)≥0.
)(x﹣2)≤0,即可解不等式f(x)≤0(2)若m>0,分类讨论解关于x的不等式f(x)≥0.
【考点精析】本题主要考查了二次函数的性质和解一元二次不等式的相关知识点,需要掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减;求一元二次不等式
上递减;求一元二次不等式![]()
![]() 解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.
解集的步骤:一化:化二次项前的系数为正数;二判:判断对应方程的根;三求:求对应方程的根;四画:画出对应函数的图象;五解集:根据图象写出不等式的解集;规律:当二次项系数为正时,小于取中间,大于取两边才能正确解答此题.

 科学实验活动册系列答案
科学实验活动册系列答案【题目】某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获得利润分别为4万元、3万元,则该企业每天可获得最大利润为万元
甲 | 乙 | 原料限额 | |
A(吨) | 2 | 5 | 10 |
B(吨) | 6 | 3 | 18 |
【题目】某青年教师有一专项课题是进行“学生数学成绩与物理成绩的关系”的研究,他调查了某中学高二年级800名学生上学期期末考试的数学和物理成绩,把成绩按优秀和不优秀分类得到的结果是:数学和物理都优秀的有60人,数学成绩优秀但物理不优秀的有140人,物理成绩优秀但数学不优秀的有60人. 附:
P(K2≥k0) | 0.100 | 0.050 | 0.010 |
k0 | 6.635 | 7.879 | 10.828 |
K2= ![]() .
.
(1)能否在犯错概率不超过0.001的前提下认为该中学学生的数学成绩与物理成绩有关?
(2)将上述调查所得到的频率视为概率,从全体高二年级学生成绩中,有放回地随机抽取4名学生的成绩,记抽取的4份成绩中数学、物理两科成绩恰有一科优秀的份数为X,求X的分布列和期望E(X).
【题目】某公司的广告费支出x与销售额y(单位:万元)之间有下列对应数据
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
回归方程为 ![]() =bx+a,其中b=
=bx+a,其中b= 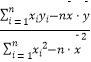 ,a=
,a= ![]() ﹣b
﹣b ![]() .
.
(1)画出散点图,并判断广告费与销售额是否具有相关关系;
(2)根据表中提供的数据,求出y与x的回归方程 ![]() =bx+a;
=bx+a;
(3)预测销售额为115万元时,大约需要多少万元广告费.