题目内容
已知函数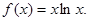
(Ⅰ)求函数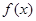 的单调区间和最小值;
的单调区间和最小值;
(Ⅱ)若函数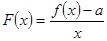 在
在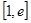 上是最小值为
上是最小值为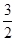 ,求
,求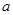 的值;
的值;
(Ⅲ)当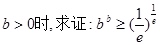 (其中
(其中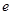 ="2.718" 28…是自然对数的底数).
="2.718" 28…是自然对数的底数).
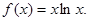
(Ⅰ)求函数
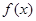 的单调区间和最小值;
的单调区间和最小值;(Ⅱ)若函数
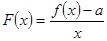 在
在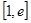 上是最小值为
上是最小值为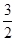 ,求
,求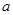 的值;
的值;(Ⅲ)当
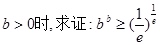 (其中
(其中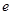 ="2.718" 28…是自然对数的底数).
="2.718" 28…是自然对数的底数).(Ⅰ)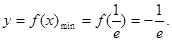 (Ⅱ)
(Ⅱ)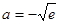 ;(Ⅲ)
;(Ⅲ)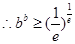 .
.
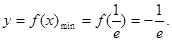 (Ⅱ)
(Ⅱ)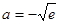 ;(Ⅲ)
;(Ⅲ)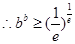 .
.(I)求导,利用导数大(小)于零,求其单调增(减)区间即可.然后再研究出极值和最值.
(II)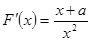 再分当
再分当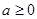 和
和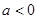 两种情况研究其单调性确定其最小值,根据最小值为
两种情况研究其单调性确定其最小值,根据最小值为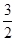 建立关于a的方程,求出a的值.
建立关于a的方程,求出a的值.
(III)解本小题的关键是由(I)可知当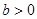 时,有
时,有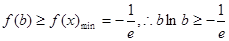 ,
,
即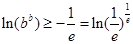 .从而可得
.从而可得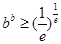 .
.
解:(Ⅰ)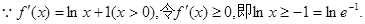
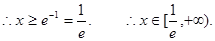
同理,令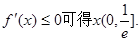
∴f(x)单调递增区间为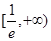 ,单调递减区间为
,单调递减区间为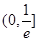 .
.
由此可知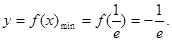
(Ⅱ)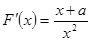
当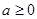 时,
时,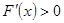 ,F(x)在
,F(x)在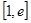 上单调递增,
上单调递增,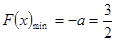 ,
,
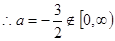 ,舍去
,舍去
当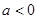 时,
时,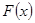 在
在 单调递减,在
单调递减,在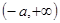 单调递增
单调递增
若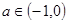 ,F(x)在
,F(x)在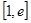 上单调递增,
上单调递增,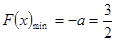 ,
,
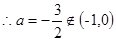 舍
舍
若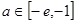 ,
,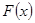 在
在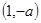 单调递减,在
单调递减,在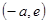 单调递增,
单调递增,
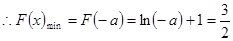 ,
,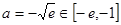
若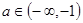 ,F(x)在
,F(x)在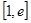 上单调递减,
上单调递减,
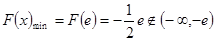 舍
舍
综上所述: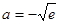
(Ⅲ)由(I)可知当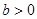 时,有
时,有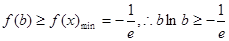 ,
,
即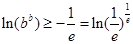 .
.
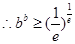 .
.
(II)
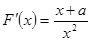 再分当
再分当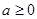 和
和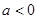 两种情况研究其单调性确定其最小值,根据最小值为
两种情况研究其单调性确定其最小值,根据最小值为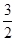 建立关于a的方程,求出a的值.
建立关于a的方程,求出a的值.(III)解本小题的关键是由(I)可知当
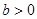 时,有
时,有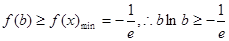 ,
,即
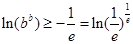 .从而可得
.从而可得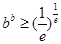 .
.解:(Ⅰ)
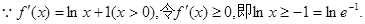
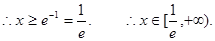
同理,令
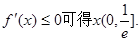
∴f(x)单调递增区间为
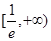 ,单调递减区间为
,单调递减区间为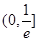 .
. 由此可知
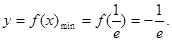
(Ⅱ)
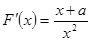
当
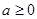 时,
时,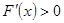 ,F(x)在
,F(x)在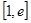 上单调递增,
上单调递增,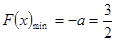 ,
,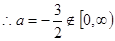 ,舍去
,舍去 当
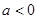 时,
时,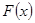 在
在 单调递减,在
单调递减,在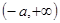 单调递增
单调递增若
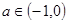 ,F(x)在
,F(x)在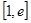 上单调递增,
上单调递增,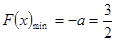 ,
,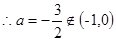 舍
舍 若
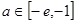 ,
,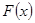 在
在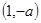 单调递减,在
单调递减,在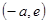 单调递增,
单调递增,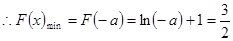 ,
,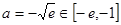
若
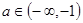 ,F(x)在
,F(x)在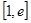 上单调递减,
上单调递减,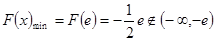 舍
舍综上所述:
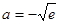
(Ⅲ)由(I)可知当
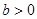 时,有
时,有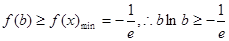 ,
,即
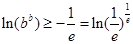 .
.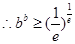 .
.
练习册系列答案
相关题目
 .
.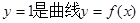 的切线,函数
的切线,函数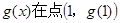 处取得极值1,求
处取得极值1,求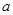 ,
,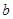 ,
,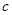 的值;
的值;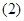 证明:
证明: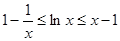 ;
; 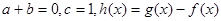 ,且函数
,且函数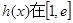 上单调递增,
上单调递增,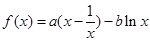 (
(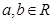 ),
),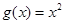 .
.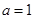 ,曲线
,曲线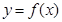 在点
在点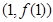 处的切线与
处的切线与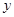 轴垂直,求
轴垂直,求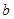 的值;
的值;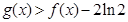 ;
;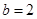 ,试探究函数
,试探究函数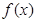 与
与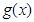 的图象在其公共点处是否存在公切线,若存在,研究
的图象在其公共点处是否存在公切线,若存在,研究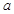 值的个数;若不存在,请说明理由.
值的个数;若不存在,请说明理由.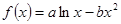 图象上一点P(2,f(2))处的切线方程为
图象上一点P(2,f(2))处的切线方程为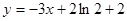 .
.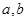 的值;
的值;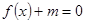 在
在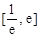 内有两个不等实根,求
内有两个不等实根,求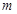 的取值范围(其中
的取值范围(其中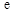 为自然对数的底);
为自然对数的底);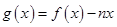 ,如果
,如果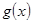 图象与
图象与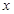 轴交于
轴交于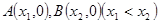 ,AB中点为
,AB中点为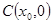 ,求证:
,求证: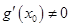 .
.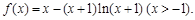
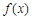 的单调区间;
的单调区间;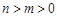 时,
时,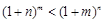 ;
;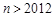 ,且
,且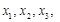 …,
…,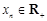 ,
,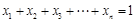 时,
时,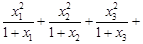 …
…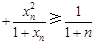
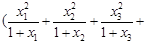 …
…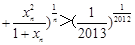 .
.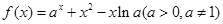 .
.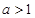 时,求证:函数
时,求证:函数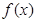 在
在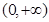 上单调递增;
上单调递增;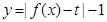 有三个零点,求
有三个零点,求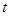 的值;
的值;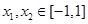 ,使得
,使得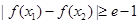 ,试求
,试求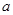 的取值范围。
的取值范围。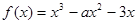 .
.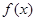 在
在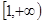 上是增函数,求实数
上是增函数,求实数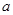 的取值范围;
的取值范围;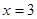 是
是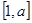 上的最小值和最大值.
上的最小值和最大值.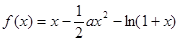 ,其中
,其中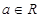 .
.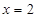 是
是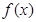 的极值点,求
的极值点,求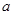 的值;
的值;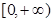 上的最大值是
上的最大值是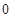 ,求
,求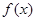 在
在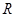 上可导,其导函数
上可导,其导函数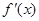 ,且函数
,且函数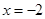 处取得极小值,
处取得极小值,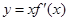 的图象可能是( )
的图象可能是( )