题目内容
19．已知数列{bn}满足b1=1，b2=5，bn+1=5bn-6bn-1，若数列{an}满足a1=1，an=bn（$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$）（n≥2，n∈N*）．（1）求证：数列{bn+1-3bn}为等比数列，并求{bn}的通项公式；
（2）求证：（1+$\frac{1}{{a}_{1}}$）（1+$\frac{1}{{a}_{2}}$）（1+$\frac{1}{{a}_{3}}$）…（1+$\frac{1}{{a}_{n}}$）＜3．
分析 （1）由{bn}满足b1=1，b2=5，bn+1=5bn-6bn-1（n≥2），知bn+1-3bn=2（bn-3bn-1），故{bn+1-3bn}成等比数列，由此能求出bn=3n-2n．
（2）由an=bn（$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$），n∈N*，推导出$\frac{{1+a}_{n}}{{a}_{n+1}}$=$\frac{{b}_{n}}{{b}_{n+1}}$，从而得到∴（1+$\frac{1}{{a}_{1}}$）（1+$\frac{1}{{a}_{2}}$）（1+$\frac{1}{{a}_{3}}$）…（1+$\frac{1}{{a}_{n}}$）=$\frac{1+{a}_{1}}{{a}_{1}}$•$\frac{1+{a}_{2}}{{a}_{2}}$•…•$\frac{{1+a}_{n}}{{a}_{n}}$=$\sum_{k=1}^{n}$$\frac{1}{{3}^{n}-{2}^{n}}$，n∈Z*．由此能够证明结论．
解答 证明：（1）∵bn+1=5bn-6bn-1，
∴bn+1-3bn=2bn-6bn-1=2（bn-3bn-1），
∴数列{bn+1-3bn}为等比数列，
又∵b1=1，b2=5，
∴b2-3b1=5-3=2，
∴bn+1-3bn=2•2n-1=2n，
∴bn+1=3bn+2n，
∴bn+1+2n+1=3（bn+2n），
又∵b1=1，∴b1+2=3，
∴bn+2n=3•3n-1=3n，
∴bn=3n-2n；
（2）∵an=bn（$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$）（n≥2，n∈N*），
∴1+an=bn（$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$）+1=bn（$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$+$\frac{1}{{b}_{n}}$），
∴$\frac{{1+a}_{n}}{{a}_{n+1}}$=$\frac{{b}_{n}（\frac{1}{{b}_{1}}+\frac{1}{{b}_{2}}+…\frac{1}{{b}_{n}}）}{{b}_{n+1}（\frac{1}{{b}_{1}}+\frac{1}{{b}_{2}}+…+\frac{1}{{b}_{n}}）}$=$\frac{{b}_{n}}{{b}_{n+1}}$，
∴（1+$\frac{1}{{a}_{1}}$）（1+$\frac{1}{{a}_{2}}$）（1+$\frac{1}{{a}_{3}}$）…（1+$\frac{1}{{a}_{n}}$）
=$\frac{1+{a}_{1}}{{a}_{1}}$•$\frac{1+{a}_{2}}{{a}_{2}}$•…•$\frac{{1+a}_{n}}{{a}_{n}}$
=$\frac{1}{{a}_{1}}$•$\frac{1+{a}_{1}}{{a}_{2}}$•$\frac{1+{a}_{3}}{{a}_{2}}$•…•$\frac{1+{a}_{n-1}}{{a}_{n}}$•（1+an）
=$\frac{1}{{a}_{1}}$•$\frac{{b}_{1}}{{b}_{2}}$•$\frac{{b}_{2}}{{b}_{3}}$•…•$\frac{{b}_{n-1}}{{b}_{n}}$•bn•（$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$+$\frac{1}{{b}_{n}}$）
=$\frac{{a}_{1}}{{b}_{1}}$•（$\frac{1}{{b}_{1}}$+$\frac{1}{{b}_{2}}$+…+$\frac{1}{{b}_{n-1}}$+$\frac{1}{{b}_{n}}$）
=$\frac{1}{1}$•（$\frac{1}{3-2}$+$\frac{1}{{3}^{2}-{2}^{2}}$+…+$\frac{1}{{3}^{n}-{2}^{n}}$）
=$\sum_{k=1}^{n}$$\frac{1}{{3}^{n}-{2}^{n}}$，
∵1-$（\frac{2}{3}）^{k}$≥$\frac{1}{3•{2}^{k-1}}$，
f（k）=1-$（\frac{2}{3}）^{k}$单调递增，
g（k）=$\frac{1}{3•{2}^{k-1}}$单调递减，
∴3k-2k≥$（\frac{3}{2}）^{k-1}$，
∴$\frac{1}{{3}^{k}-{2}^{k}}$≤$（\frac{2}{3}）^{k-1}$，
∴$\sum_{k=1}^{n}$$\frac{1}{{3}^{n}-{2}^{n}}$≤$\sum_{k=1}^{n}$$（\frac{2}{3}）^{k-1}$=$\frac{1}{1-\frac{2}{3}}$=3，
∴（1+$\frac{1}{{a}_{1}}$）（1+$\frac{1}{{a}_{2}}$）（1+$\frac{1}{{a}_{3}}$）…（1+$\frac{1}{{a}_{n}}$）＜3．
点评 本题考查等比数列的证明，考查数列的通项公式的求法，考查不等式的证明．解题时要认真审题，注意构造法和等价转化思想的合理运用，属于中档题．
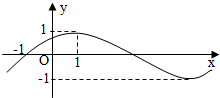已知函数f（x）=Asin（ωx+ϕ），x∈R（其中A＞0，ω＞0，-$\frac{π}{2}$＜ϕ＜$\frac{π}{2}$），其部分图象如下图所示，将f（x）的图象纵坐标不变，横坐标变成原来的$\frac{1}{2}$倍，再向右平移1个单位得到g（x）的图象，则函数g（x）的解析式为（ ）| A． | g（x）=sin$\frac{π}{8}$（x+1） | B． | g（x）=sin（$\frac{π}{2}$x-$\frac{π}{4}$） | C． | g（x）=sin（$\frac{π}{8}$x+1） | D． | g（x）=sin（$\frac{π}{2}$x+$\frac{π}{4}$） |