题目内容
4.在数列{an}中,a1=2,an+1=2a${\;}_{n}^{2}$,bn=log2an,求证:数列{bn+1}是等比数列.分析 通过an+1=2a${\;}_{n}^{2}$,利用对数的性质可得bn+1=1+2bn,变形可得1+bn+1=2(1+bn),进而可得结论.
解答 证明:∵an+1=2a${\;}_{n}^{2}$,bn=log2an,
∴bn+1=log2an+1
=log22a${\;}_{n}^{2}$
=log22+$lo{g}_{2}{{a}_{n}}^{2}$
=1+2log2an
=1+2bn,
∴1+bn+1=2(1+bn),
即数列{bn+1}是以2为公比的等比数列.
∵a1=2,
∴b1=log2a1=log22=1,
∴1+bn=(1+1)•2n-1=2n.
点评 本题考查等比数列的判定,注意解题方法的积累,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.若a,b∈{-1,0,1,2},则函数f(x)=ax2+2x+b没有零点的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{5}{8}$ | C. | $\frac{13}{16}$ | D. | $\frac{3}{16}$ |
13.sin45°cos15°-cos135°sin165°=( )
| A. | -$\frac{1}{2}$ | B. | -$\frac{\sqrt{3}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
14.函数f(x)=$\frac{1}{\sqrt{lo{g}_{\frac{1}{2}}(2x-3)}}$的定义域为( )
| A. | ($\frac{3}{2}$,+∞) | B. | (2,+∞) | C. | (0,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,2) |
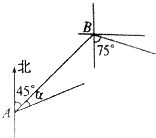 中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.
中国渔政310船在一次巡航执法作业中,发现在北偏东45°方向,相距12海里的水面上,有一艘不明国籍渔船正以每小时10海里的速度沿南偏东75°方向前进,中国渔政310船以每小时14海里的速度沿北偏东45°+α方向拦截该渔船,若要在最短的时间内拦截住,求中国渔政310船所需的时间和角α的正弦值.