题目内容
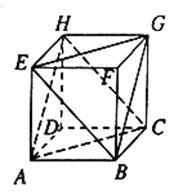
【题目】正方体![]() 的直观图如图所示:
的直观图如图所示:
(1)判断平面![]() 与平面
与平面![]() 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
(2)证明:直线![]() 平面
平面![]() .
.
(3)若![]() ,求点
,求点![]() 到面
到面![]() 的距离.
的距离.
【答案】(1)平行,见解析;(2)见解析;(3)![]() .
.
【解析】
(1)可证![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,利用面面平行的判定定理可得平面
,利用面面平行的判定定理可得平面![]() 与平面
与平面![]() 平行.
平行.
(2)可证![]() ,
,![]() ,由线面垂直的判定定理可得直线
,由线面垂直的判定定理可得直线![]() 平面
平面![]() .
.
(3)利用等积法可求点![]() 到面
到面![]() 的距离.
的距离.
(1)平面![]() 平面
平面![]() ,证明如下:
,证明如下:
因为![]() 为正方体,
为正方体,
所以![]() ,
,![]() ,
,
又![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,
于是![]() 为平行四边形,所以
为平行四边形,所以![]() ,
,
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,同理
,同理![]() 平面
平面![]() ,
,
又![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)

证明: 连接![]() ,因为
,因为![]() 为正方体,
为正方体,
所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,
,![]() ,
,
所以![]() 平面
平面![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() ,
,
同理![]() ,又
,又![]() ,
,
所以![]() 平面
平面![]() .
.
(3)设![]() 到平面
到平面![]() 距离为
距离为![]() ,
,
由正方体![]() 可得
可得![]() 为等边三角形,且边长为
为等边三角形,且边长为![]() ,
,
故![]() ,
,
![]() ,故
,故![]() ,故
,故![]() .
.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
【题目】4月23日是“世界读书日”,某中学开展了一系列的读书教育活动.学校为了解高三学生课外阅读情况,采用分层抽样的方法从高三某班甲、乙、丙、丁四个读书小组(每名学生只能参加一个读书小组)学生抽取12名学生参加问卷调查.各组人数统计如下:
小组 | 甲 | 乙 | 丙 | 丁 |
人数 | 12 | 9 | 6 | 9 |
(1)从参加问卷调查的12名学生中随机抽取2人,求这2人来自同一个小组的概率;
(2)从已抽取的甲、丙两个小组的学生中随机抽取2人,用![]() 表示抽得甲组学生的人数,求随机变量
表示抽得甲组学生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
