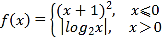题目内容
【题目】已知函数
,其中
是实数。设
, 
为该函数图象上的两点,且
，若函数
的图象在点
处的切线重合,则的取值范围为（ ）
A. 
B. 
C. 
D. 
【答案】A
【解析】
先根据导数的几何意义写出函数f（x）在点A、B处的切线方程，再利用两直线重合的充要条件列出关系式，从而得出a=lnx2+（
﹣1）2﹣1，最后利用导数研究它的单调性和最值，即可得出a的取值范围．
当x1＜x2＜0，或0＜x1＜x2时，f′（x1）≠f′（x2），故x1＜0＜x2，
当x1＜0时，函数f（x）在点A（x1，f（x1））处的切线方程为y﹣（x12+2x1+a）=（2x1+2）（x﹣x1）；
当x2＞0时，函数f（x）在点B（x2，f（x2））处的切线方程为y﹣lnx2=
（x﹣x2）；
两直线重合的充要条件是=2x1+2①，lnx2﹣1=﹣x12+a②，
由①及x1＜0＜x2得0＜＜2，由①②得a=lnx2+（﹣1）2﹣1=﹣ln+
（﹣2）2﹣1，
令t=，则0＜t＜2，且a=t2﹣t﹣lnt，设h（t）=t2﹣t﹣lnt，（0＜t＜2）
则h′（t）=
t﹣1﹣
=
＜0，∴h（t）在（0，2）为减函数，
则h（t）＞h（2）=﹣ln2﹣1，∴a＞﹣ln2﹣1，
∴若函数f（x）的图象在点A，B处的切线重合，a的取值范围（﹣ln2﹣1，+∞）．
故选：A．
练习册系列答案
相关题目
