题目内容
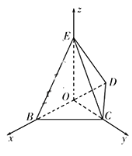
【题目】如图,菱形ABCD中,AB=4,∠A=60°,以对角线BD为折痕把△ABD折起,使点A到达如图所示点E的位置,使![]() .
.
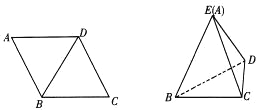
(1)求证:BD⊥EC;
(2)求三棱锥B-CE-D的余弦值.
【答案】(1)见解析;(2)二面角B-CE-D的余弦值为![]() .
.
【解析】
(1)根据菱形的对角线相互垂直,得到CO⊥BD且AO⊥BD,所以BD⊥平面EOC,从而得证;
(2)先证明OB,OC,OE三者两两垂直,以O为坐标原点.OB,OC,OE所在直线分别x、y、z轴建立空间直角坐标系O – xyz,求出平面BCE与平面CDE的法向量,代入公式即可得到结果.
(1)在图1中,连接A、C,设AC与BD相交于点O,由四边形ABCD为菱形可知![]() ,所以
,所以![]() ,由图2可知
,由图2可知
![]() ,
,
又![]() ,所以
,所以![]() 平面EOC,又
平面EOC,又![]() 平面EOC,所以
平面EOC,所以![]() .
.
(2)因为四边形ABCD为菱形且![]() ,所以
,所以![]() 为等边三角形
为等边三角形
又![]() ,所以
,所以![]() .所以
.所以![]() .
.
又![]() 中,
中,![]() ,所以
,所以![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,因为
,因为![]() ,所以
,所以![]() 平面BDC,所以OB,OC,OE三者两两垂直.
平面BDC,所以OB,OC,OE三者两两垂直.
以O为坐标原点.OB,OC,OE所在直线分别x、y、z轴建立空间直角坐标系O – xyz,
则![]() ,
,
![]() .
.
设平面BCE的法向量为![]()
由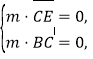 得
得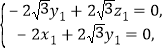 所以
所以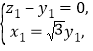
令![]() 得
得![]() ;
;
设平面CDE的法向量为![]() ,
,
由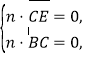 得
得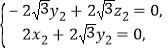 所以
所以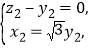 令
令![]() 得
得![]() ;故
;故![]() ,
,
由图可知二面角B-CE-D为锐角,所以二面角B-CE-D的余弦值为![]()

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目