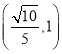题目内容
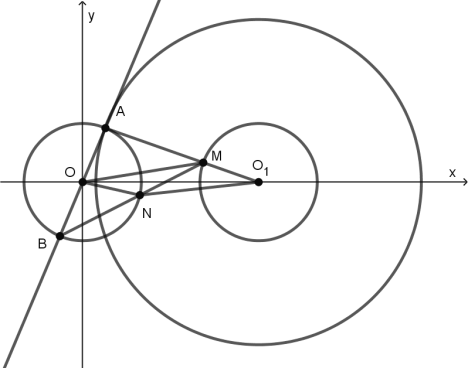
【题目】在平面直角坐标系xOy中,AB是圆O:x2+y2=1的直径,且点A在第一象限;圆O1:(x﹣a)2+y2=r2(a>0)与圆O外离,线段AO1与圆O1交于点M,线段BM与圆O交于点N,且![]() ,则a的取值范围为_______.
,则a的取值范围为_______.
【答案】![]()
【解析】
根据![]() 判断出四边形
判断出四边形![]() 为平行四边形,由此求得圆
为平行四边形,由此求得圆![]() 的方程以及
的方程以及![]() 的长,进而判断出
的长,进而判断出![]() 点在圆
点在圆![]() 上,根据圆
上,根据圆![]() 与圆
与圆![]() 的位置关系,求得
的位置关系,求得![]() 的取值范围.
的取值范围.
![]() 四边形ONO1M为平行四边形,即ON=MO1=r=1,
四边形ONO1M为平行四边形,即ON=MO1=r=1,
所以圆![]() 的方程为
的方程为![]() ,
,
且ON为△ABM的中位线![]() AM=2ON=2
AM=2ON=2![]() AO1=3,
AO1=3,
故点A在以O1为圆心,3为半径的圆上,该圆的方程为:![]() ,
,
故![]() 与x2+y2=1在第一象限有交点,即2<a<4,
与x2+y2=1在第一象限有交点,即2<a<4,
由 ,解得
,解得![]() ,
,
故a的取值范围为(![]() ,4).
,4).
故答案为:![]()

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目