题目内容
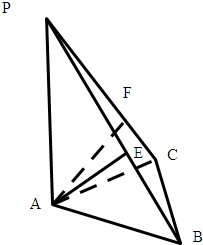
三棱锥P-ABC,PA⊥面ABC,AC⊥BC,点E、F分别是A在PB、PC上的射影,则( )
| A.∠EAF是二面角B-PA-C的平面角 |
| B.∠AFE是二面角A-PC-B的平面角 |
| C.∠FEA是二面角C-PB-A的平面角 |
| D.∠PCB是二面角P-AC-B的平面角 |
如图,∵三棱锥P-ABC,PA⊥面ABC
∴PA⊥BC,又AC⊥BC
由线面垂直的定理知BC⊥面PAC,又AF?面PAC,可得AF⊥BC
又点E、F分别是A在PB、PC上的射影可得AF⊥PC,AE⊥PB
又BC∩PC=C
∴AF⊥面PCB,可AF⊥PB
∴PB⊥面FEA,
故角AEF即为二面角C-PB-A的平面角
故选C
∴PA⊥BC,又AC⊥BC
由线面垂直的定理知BC⊥面PAC,又AF?面PAC,可得AF⊥BC
又点E、F分别是A在PB、PC上的射影可得AF⊥PC,AE⊥PB
又BC∩PC=C
∴AF⊥面PCB,可AF⊥PB
∴PB⊥面FEA,
故角AEF即为二面角C-PB-A的平面角
故选C


练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 中,平面
中,平面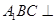 侧面
侧面 ,且
,且
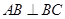 ;
; 与平面
与平面 所成的角为
所成的角为 ,求锐二面角
,求锐二面角 的大小。
的大小。

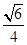



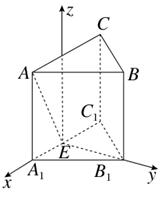
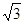 ,则异面直线AD,BC所成的角为( )
,则异面直线AD,BC所成的角为( )