题目内容
19.sin$\frac{22π}{3}$等于( )| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
分析 由条件利用诱导公式进行化简所给的式子,可得结果.
解答 解:sin$\frac{22π}{3}$=sin(8π-$\frac{2}{3}$π)=-sin$\frac{2π}{3}$=-sin$\frac{π}{3}$=-$\frac{\sqrt{3}}{2}$,
故选:D.
点评 本题主要考查利用诱导公式进行化简求值,属于基础题.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
9.有下列四个命题:
①“平面内一个动点到两个定点的距离之和为定长,则动点的轨迹为椭圆”;
②“若q≤1,则方程x2+2x+q=0有实根”的否命题;
③“若m>1,则mx2-2(m+1)x+m+3>0的解集为R”的逆命题.
④“若两条直线没有公共点,则这两条直线是异面直线”的逆否命题.
其中真命题的序号有( )
①“平面内一个动点到两个定点的距离之和为定长,则动点的轨迹为椭圆”;
②“若q≤1,则方程x2+2x+q=0有实根”的否命题;
③“若m>1,则mx2-2(m+1)x+m+3>0的解集为R”的逆命题.
④“若两条直线没有公共点,则这两条直线是异面直线”的逆否命题.
其中真命题的序号有( )
| A. | ②③ | B. | ①③④ | C. | ①③ | D. | ①④ |
10.设$a={log_2}π,b={log_{\frac{1}{2}}}π,c=\frac{1}{π^2}$则( )
| A. | a>b>c | B. | b>a>c | C. | a>c>b | D. | c>b>a |
14.在如图所示的平面图形中,$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为互相垂直的单位向量,则向量$\overrightarrow{a}$+$\overrightarrow{b}$-$\overrightarrow{c}$可表示为( )
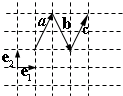
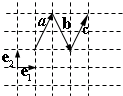
| A. | $\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | B. | -$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$ | C. | -$\overrightarrow{{e}_{1}}$-2$\overrightarrow{{e}_{2}}$ | D. | 3$\overrightarrow{{e}_{1}}$+2$\overrightarrow{{e}_{2}}$ |
9.数列-1,$\frac{8}{5}$,-$\frac{15}{7}$,$\frac{24}{9}$,…的一个通项公式an是( )
| A. | (-1)n$\frac{{n}^{2}}{2n+1}$ | B. | (-1)n$\frac{n(n+2)}{n+1}$ | C. | (-1)n$\frac{n(n+2)}{2n+1}$ | D. | (-1)n$\frac{(n+1)^{2}-1}{2(n+1)}$ |