题目内容
【题目】已知椭圆C:![]() 的离心率
的离心率![]() ,连接椭圆的四个顶点得到的菱形的面积为
,连接椭圆的四个顶点得到的菱形的面积为![]() .
.

![]() 求椭圆C的方程;
求椭圆C的方程;
![]() 如图所示,该椭圆C的左、右焦点
如图所示,该椭圆C的左、右焦点![]() ,
,![]() 作两条平行的直线分别交椭圆于A,B,C,D四个点,试求平行四边形ABCD面积的最大值.
作两条平行的直线分别交椭圆于A,B,C,D四个点,试求平行四边形ABCD面积的最大值.
【答案】(1)![]() ;(2) 最大值为
;(2) 最大值为![]() .
.
【解析】
![]() 由题意离心率可得
由题意离心率可得![]() ,再结合面积求解a,b的值,则椭圆方程可求;
,再结合面积求解a,b的值,则椭圆方程可求;
![]() 由
由![]() 知,
知,![]() ,且直线AB的斜率不为0,设直线AB的方程为
,且直线AB的斜率不为0,设直线AB的方程为![]() ,联立直线方程与椭圆方程,把平行四边形ABCD的面积用三角形OAB的面积表示,然后利用换元法结合单调性求最值.
,联立直线方程与椭圆方程,把平行四边形ABCD的面积用三角形OAB的面积表示,然后利用换元法结合单调性求最值.
解:![]() 由题意,
由题意,![]() ,则
,则![]() ,即
,即![]() .
.
又![]() ,
,![]() ,
,![]() .
.
![]() 椭圆C的方程为
椭圆C的方程为![]() ;
;
![]() 由
由![]() 知,
知,![]() ,且直线AB的斜率不为0,
,且直线AB的斜率不为0,
设直线AB的方程为![]() ,
,![]() ,
,![]() ,
,
联立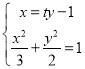 ,消去x得:
,消去x得:![]() .
.
得![]() ,
,![]() .
.
![]() 四边形
四边形![]() 是平行四边形,根据对称性可知
是平行四边形,根据对称性可知![]() 和
和![]() 关于点
关于点![]() 对称,
对称,
![]()
![]()
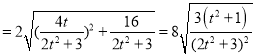 .
.
令![]() ,则
,则![]() ,
,
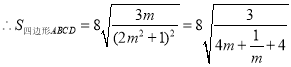 .
.
![]() ,且函数
,且函数![]() 在
在![]() 上单调递增,
上单调递增,
![]() 当
当![]() ,即
,即![]() 时,平行四边形ABCD面积的最大值为
时,平行四边形ABCD面积的最大值为![]() .
.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目

