题目内容
【题目】某厂使用两种零件![]() 、
、![]() 装配两种产品
装配两种产品![]() 、
、![]() ,该厂的生产能力是月产
,该厂的生产能力是月产![]() 产品最多有2500件,月产
产品最多有2500件,月产![]() 产品最多有1200件;而且组装一件
产品最多有1200件;而且组装一件![]() 产品要4个
产品要4个![]() 、2个
、2个![]() ,组装一件
,组装一件![]() 产品要6个
产品要6个![]() 、8个
、8个![]() ,该厂在某个月能用的
,该厂在某个月能用的![]() 零件最多14000个;
零件最多14000个;![]() 零件最多12000个.已知
零件最多12000个.已知![]() 产品每件利润1000元,
产品每件利润1000元,![]() 产品每件2000元,欲使月利润最大,需要组装
产品每件2000元,欲使月利润最大,需要组装![]() 、
、![]() 产品各多少件?最大利润多少万元?
产品各多少件?最大利润多少万元?
【答案】要使月利润最大,需要组装![]() 、
、![]() 产品2000件、1000件,此时最大利润为400万元
产品2000件、1000件,此时最大利润为400万元
【解析】
设分别生产![]() 、
、![]() 产品
产品![]() 件、
件、![]() 件,根据题设条件可得
件,根据题设条件可得![]() 满足的不等式组且利润
满足的不等式组且利润![]() ,利用线性规划可求
,利用线性规划可求![]() 的最大值及取最大值时对应的
的最大值及取最大值时对应的![]() 的值.
的值.
设分别生产![]() 、
、![]() 产品
产品![]() 件、
件、![]() 件,则有
件,则有
依题意有 .
.
设利润为![]() ,则
,则![]() ,
,
要使利润最大,只需求![]() 的最大值.
的最大值.
作出可行域如图所示(阴影部分及边界):
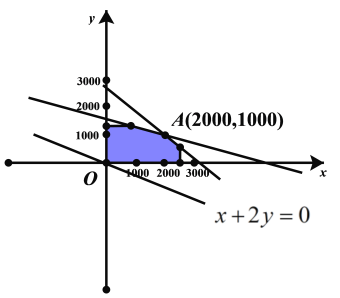
作出直线![]() :
:![]() ,即
,即![]() ,
,
由于向上平移直线![]() 时,
时,![]() 的值增大,所以在点
的值增大,所以在点![]() 处
处![]() 取得最大值,
取得最大值,
由![]() 解得
解得![]() ,即
,即![]() ,
,
因此,此时最大利润![]() (万元)..
(万元)..
答:要使月利润最大,需要组装![]() 、
、![]() 产品2000件、1000件,此时最大利润为400万元.
产品2000件、1000件,此时最大利润为400万元.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

