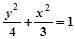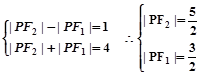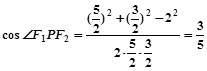题目内容
已知椭圆的两焦点是F1(0,-1),F2(0,1),离心率e=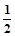
(1)求椭圆方程;(2)若P在椭圆上,且|PF1|-|PF2|=1,求cos∠F1PF2。
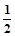
(1)求椭圆方程;(2)若P在椭圆上,且|PF1|-|PF2|=1,求cos∠F1PF2。
(1)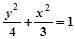 (2)
(2)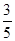
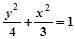 (2)
(2)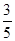
试题分析:(1)c=1
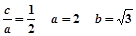 椭圆方程为
椭圆方程为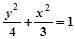
(2)
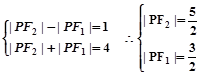
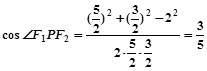
点评:解决的关键是对于椭圆的性质的熟练运用,以及定义和解三角形的综合运用,属于基础题。

练习册系列答案
相关题目
题目内容
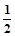
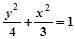 (2)
(2)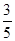
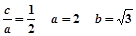 椭圆方程为
椭圆方程为