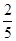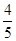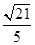题目内容
已知椭圆的长轴长为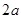 ,焦点是
,焦点是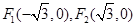 ,点
,点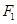 到直线
到直线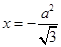 的距离为
的距离为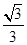 ,过点
,过点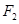 且倾斜角为锐角的直线
且倾斜角为锐角的直线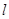 与椭圆交于
与椭圆交于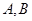 两点,使得
两点,使得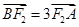 .
.
(1)求椭圆的方程;(2)求直线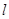 的方程.
的方程.
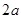 ,焦点是
,焦点是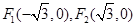 ,点
,点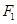 到直线
到直线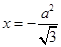 的距离为
的距离为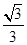 ,过点
,过点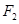 且倾斜角为锐角的直线
且倾斜角为锐角的直线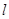 与椭圆交于
与椭圆交于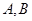 两点,使得
两点,使得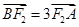 .
.(1)求椭圆的方程;(2)求直线
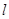 的方程.
的方程.(1)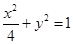 (2)
(2)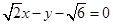
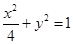 (2)
(2)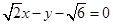
试题分析:(1)∵
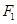 到直线
到直线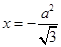 的距离为
的距离为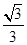 ,∴
,∴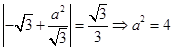 .
.而
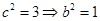 ,所求椭圆的方程为
,所求椭圆的方程为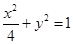 . 5分
. 5分(2)设
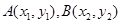 ,∵
,∵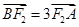 ,∴
,∴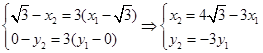
由∵
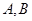 在椭圆
在椭圆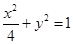 上,∴
上,∴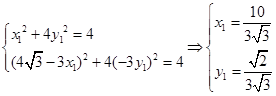 (取正值)
(取正值)∴
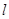 的斜率为
的斜率为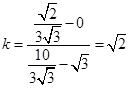 。∴
。∴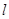 的方程为
的方程为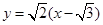 ,即
,即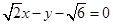 。
。点评:第二问中的向量关系式常用坐标表示,转化为坐标运算,所以本题还可首先设出直线
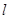 方程,与椭圆联立找到根与系数的关系,再结合向量的坐标表示求得交点,从而确定直线
方程,与椭圆联立找到根与系数的关系,再结合向量的坐标表示求得交点,从而确定直线
练习册系列答案
相关题目
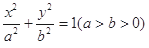 .
.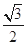 ,求椭圆的标准方程;
,求椭圆的标准方程;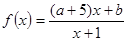 在
在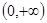 上是增函数;命题q:方程
上是增函数;命题q:方程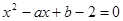 有两个不相等的负实数根。求使得p
有两个不相等的负实数根。求使得p q是真命题的实数对
q是真命题的实数对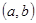 为坐标的点的轨迹图形及其面积。
为坐标的点的轨迹图形及其面积。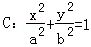 的右焦点F,抛物线:
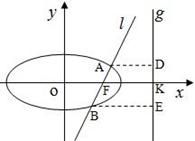
的右焦点F,抛物线: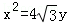 的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且
的焦点为椭圆C的上顶点,且直线l交椭圆C于A、B两点,点A、F、B在直线g:x=4上的射影依次为点D、K、E.(1)椭圆C的方程;(2)直线l交y轴于点M,且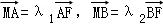 ,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点
,当m变化时,探求λ1+λ2的值是否为定值?若是,求出λ1+λ2的值,否则,说明理由;(3)接AE、BD,试证明当m变化时,直线AE与BD相交于定点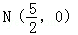 .
.
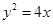 的焦点作直线
的焦点作直线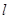 交抛物线于
交抛物线于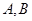 两点,若线段
两点,若线段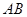 中点的横坐标为3,则
中点的横坐标为3,则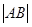 等于___________.
等于___________. 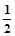
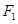 和
和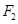 分别是双曲线
分别是双曲线 (
(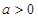 ,
, )的两个焦点,
)的两个焦点,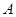 和
和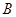 是以
是以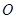 为圆心,以
为圆心,以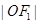 为半径的圆与该双曲线左支的两个交点,且
为半径的圆与该双曲线左支的两个交点,且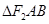 是等边三角形,则该双曲线的离心率为( )
是等边三角形,则该双曲线的离心率为( )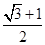
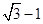
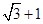
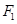 ,
,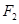 是椭圆
是椭圆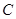 的两个焦点,焦距为4.若
的两个焦点,焦距为4.若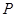 为椭圆
为椭圆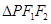 的周长为14,则椭圆
的周长为14,则椭圆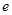 为
为