题目内容
【题目】已知![]() 为单位正方体,黑白两只蚂蚁从点
为单位正方体,黑白两只蚂蚁从点![]() 出发沿棱向前爬行,每走完一条棱称为“走完一段”,白蚂蚁爬行的路线是
出发沿棱向前爬行,每走完一条棱称为“走完一段”,白蚂蚁爬行的路线是![]() ,黑蚂蚁爬行的路线是
,黑蚂蚁爬行的路线是![]() ,它们都遵循如下规则:所爬行的第
,它们都遵循如下规则:所爬行的第![]() 段与第
段与第![]() 段所在直线必须是异面直线(其中
段所在直线必须是异面直线(其中![]() 是自然数),设黑、白蚂蚁都走完2012段后各停止在正方体的某个顶点处,这时黑、白两只蚂蚁的距离是______________.
是自然数),设黑、白蚂蚁都走完2012段后各停止在正方体的某个顶点处,这时黑、白两只蚂蚁的距离是______________.
【答案】![]()
【解析】
根据已知条件先分析出黑、白蚁路线的规律,然后考虑走完![]() 段相当于走了多少个周期,从而确定出最终位置即可求解出黑、白两蚁的距离.
段相当于走了多少个周期,从而确定出最终位置即可求解出黑、白两蚁的距离.
因为蚂蚁爬行的第![]() 段与第
段与第![]() 段所在直线必须是异面直线,
段所在直线必须是异面直线,
所以白蚁的路线如下图所示(红色部分):![]() ,
,
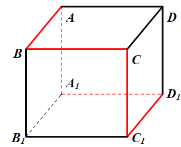
所以黑蚁的路线如下图所示(红色部分):![]() ,
,
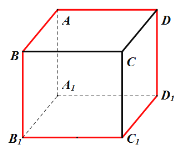
由图可知:白蚁每行走![]() 段为一个周期,黑蚁也每行走
段为一个周期,黑蚁也每行走![]() 段为一个周期,且
段为一个周期,且![]() ,
,
所以黑白两蚁走完第![]() 段所在位置和走完第
段所在位置和走完第![]() 段所在位置相同,
段所在位置相同,
所以白蚁在![]() 点,黑蚁在
点,黑蚁在![]() 点,且
点,且![]() ,
,
所以黑、白两只蚂蚁的距离是![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目
【题目】某中学用简单随机抽样方法抽取了100名同学,对其社会实践次数进行调查,结果如下:
|
|
|
|
|
|
|
男同学人数 | 7 | 15 | 11 | 12 | 2 | 1 |
女同学人数 | 5 | 13 | 20 | 9 | 3 | 2 |
若将社会实践次数不低于12次的学生称为“社会实践标兵”.
(Ⅰ)将频率视为概率,估计该校1600名学生中“社会实践标兵”有多少人?
(Ⅱ)从已抽取的8名“社会实践标兵”中随机抽取4位同学参加社会实践表彰活动.
(i)设![]() 为事件“抽取的4位同学中既有男同学又有女同学”,求事件
为事件“抽取的4位同学中既有男同学又有女同学”,求事件![]() 发生的概率;
发生的概率;
(ii)用![]() 表示抽取的“社会实践标兵”中男生的人数,求随机变量
表示抽取的“社会实践标兵”中男生的人数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.