题目内容
【题目】蝴蝶定理因其美妙的构图,像是一只翩翩起舞的蝴蝶,一代代数学名家蜂拥而证,正所谓花若芬芳蜂蝶自来.如图,已知圆![]() 的方程为
的方程为![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() ,直线
,直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() .原点
.原点![]() 在圆
在圆![]() 内.
内.

(1)求证:![]() .
.
(2)设![]() 交
交![]() 轴于点
轴于点![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .求证:
.求证:![]() .
.
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)联立直线方程和圆的方程,求出两根之和与两根之积,找到相等代换量,从而证明成立.
(2)分别求出点![]() 和点
和点![]() 的横坐标表达式,结合(1)中得证结论,从而证明成立.
的横坐标表达式,结合(1)中得证结论,从而证明成立.
(1)已知圆![]() 的方程为
的方程为![]() ,
,
直线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() ,联立
,联立 ,
,
化简得![]() ,
,
则![]() ,
,![]() ,所以
,所以![]() ,
,
同理线![]() 与圆
与圆![]() 交于
交于![]() ,
,![]() ,
,
联立 化简得
化简得![]() ,
,
则![]() ,
,![]() ,所以
,所以![]() ,
,
故有![]() ,所以
,所以![]() 成立;
成立;
(2)不妨设点![]() ,点
,点![]() ,
,
因为![]() 、
、![]() 、
、![]() 三点共线,所以
三点共线,所以![]() ,化简得
,化简得![]() ,
,
因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,点
,点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,
,
则![]() ,
,
同理因为![]() 、
、![]() 、
、![]() 三点共线,所以
三点共线,所以![]() ,化简得
,化简得![]() ,
,
因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,点
,点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,
,
则![]() ,
,
又由![]() ,可得
,可得![]() ,
,![]() ,
,
即![]() ,所以
,所以![]() ,则
,则![]() ,
,
所以![]() ,所以
,所以![]() 成立.
成立.

【题目】教育学家分析发现加强语文阅读理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同类班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)
优秀人数 | 非优秀人数 | 总计 | |
甲班 |
|
|
|
乙班 |
|
|
|
总计 |
|
|
|
(1)能否据此判断有![]() 把握认为加强语文阅读训练与提高数学应用题得分率有关?
把握认为加强语文阅读训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学应用题所用的时间在![]() 分钟,小刚正确解答一道数学应用题所用的时间在
分钟,小刚正确解答一道数学应用题所用的时间在![]() 分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明先正确解答完的概率;
(3)现从乙班成绩优秀的![]() 名同学中任意抽取两人,并对他们的答题情况进行全程研究,记
名同学中任意抽取两人,并对他们的答题情况进行全程研究,记![]() 两人中被抽到的人数为
两人中被抽到的人数为![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
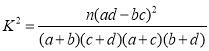
【题目】有甲、乙两个班级进行数学考试,按照大于等于85分为优秀,85分以下为非优秀统计成绩,得到如下所示的列联表:
优秀 | 非优秀 | 总计 | |
甲班 | 10 |
| |
乙班 |
| 30 | |
总计 |
|
已知在全部105人中随机抽取1人,成绩优秀的概率为![]() ,则下列说法正确的是( )
,则下列说法正确的是( )
A. 列联表中![]() 的值为30,
的值为30,![]() 的值为35
的值为35
B. 列联表中![]() 的值为15,
的值为15,![]() 的值为50
的值为50
C. 根据列联表中的数据,若按![]() 的可靠性要求,能认为“成绩与班级有关系”
的可靠性要求,能认为“成绩与班级有关系”
D. 根据列联表中的数据,若按![]() 的可靠性要求,不能认为“成绩与班级有关系”
的可靠性要求,不能认为“成绩与班级有关系”