题目内容
【题目】对于在区间![]() 上有意义的两个函数
上有意义的两个函数![]() 与
与![]() ,如果对任意的
,如果对任意的![]() ,均有
,均有![]() ,则称
,则称![]() 与
与![]() 在
在![]() 上是接近的,否则称
上是接近的,否则称![]() 与
与![]() 在
在![]() 上是非接近的.现在有两个函数
上是非接近的.现在有两个函数![]() 与
与![]() ,现给定区间
,现给定区间![]() .
.
(1)若![]() ,判断
,判断![]() 与
与![]() 是否在给定区间上接近;
是否在给定区间上接近;
(2)是否存在![]() ,使得
,使得![]() 与
与![]() 在给定区间
在给定区间![]() 上是接近的;若存在,求
上是接近的;若存在,求![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(1)不是;(2)![]() .
.
【解析】
试题分析:(1)当![]() 时,
时,![]() 在
在![]() 上的值域,即可;(2)利用反证法:假设
上的值域,即可;(2)利用反证法:假设![]() 与
与![]() 在给定区间
在给定区间![]() 上是接近的,由
上是接近的,由![]() 可得
可得![]() ,考查函数
,考查函数![]() 在
在![]() 上的单调性,从而可求
上的单调性,从而可求![]() ,
,![]() ,则有
,则有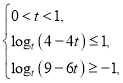 ,可求.
,可求.
试题解析:(1)当![]() 时,
时,![]() ,
,
令![]() ,当
,当![]() 时,
时,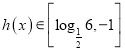
![]()
![]() ,即
,即![]() 与
与![]() 在给定区间上是非接近的.………………(4分)
在给定区间上是非接近的.………………(4分)
(2)![]() 与
与![]() 在给定区间
在给定区间![]() 上有意义,
上有意义,
由题意知,![]() 且
且![]() ,
,
![]() .………………(5分)
.………………(5分)
![]() .
.
若![]() 与
与![]() 在给定区间
在给定区间![]() 上是接近的,
上是接近的,
则有![]() ,
,![]() (*)
(*)
令![]()
![]() 当
当![]() 时,
时,![]() 在对称轴
在对称轴![]() 的右侧,
的右侧,
即![]() 在
在![]() 上为减函数,
上为减函数,
![]() ,
,![]() ………………(10分)
………………(10分)
所以由(*)式可得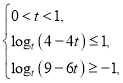 解得
解得![]() .
.
综上,两函数在给定区间是接近的,则的取值范围为:![]() .………………(12分)
.………………(12分)

练习册系列答案
相关题目
【题目】某电视台在一次对收看文艺节目和新闻节目观众的抽样调查中,随机抽取了100 名电视观众,相关的数据如下表(单位:人)所示:
收看文艺节目 | 收看新闻节目 | 总计 | |
20至40岁 | 40 | 18 | 58 |
大于40岁 | 15 | 27 | 42 |
总计 | 55 | 45 | 100 |
由表中数据直观分析,收看新闻节目的观众是否与年龄有关:__________.(填“是”或“否”)
