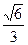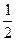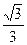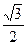题目内容
.(本小题满分13分)
已知椭圆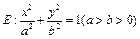 的焦点为
的焦点为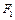 ,
,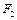 ,
,
离心率为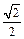 ,直线
,直线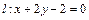 与
与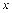 轴,
轴,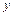 轴分别交于点
轴分别交于点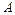 ,
,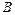 .
.
(Ⅰ)若点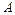 是椭圆
是椭圆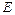 的一个顶点,求椭圆
的一个顶点,求椭圆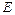 的方程;
的方程;
(Ⅱ)若线段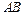 上存在点
上存在点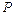 满足
满足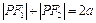 ,求
,求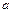 的取值范围.
的取值范围.
已知椭圆
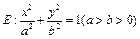 的焦点为
的焦点为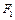 ,
,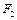 ,
, 离心率为
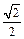 ,直线
,直线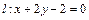 与
与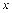 轴,
轴,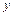 轴分别交于点
轴分别交于点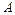 ,
,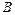 .
.(Ⅰ)若点
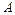 是椭圆
是椭圆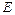 的一个顶点,求椭圆
的一个顶点,求椭圆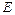 的方程;
的方程;(Ⅱ)若线段
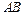 上存在点
上存在点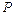 满足
满足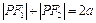 ,求
,求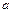 的取值范围.
的取值范围.解法一:(Ⅰ)由椭圆的离心率为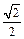 ,故
,故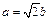 , …………………1分
, …………………1分
由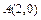 ,得
,得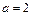 , ∴
, ∴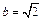 , …………………4分
, …………………4分
所以所求的椭圆方程为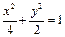 . …………………5分
. …………………5分
(Ⅱ)由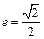 ,可设椭圆方程为
,可设椭圆方程为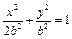 ,
,
联立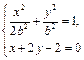 得
得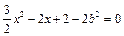 , …………………7分
, …………………7分
已知线段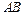 上存在点
上存在点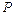 满足
满足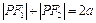 ,即线段
,即线段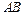 与椭圆
与椭圆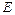 有公共点,
有公共点,
等价于方程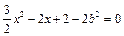 在
在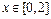 上有解.………………9分
上有解.………………9分
∴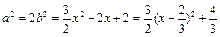 ,
,
由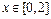 ,故
,故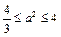 ,
,
故所求的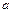 的取值范围是
的取值范围是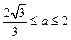 . …………………13分
. …………………13分
解法二:(Ⅰ)同解法一;
(Ⅱ)由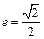 ,设椭圆方程为
,设椭圆方程为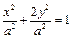 ,
,
联立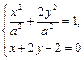 得
得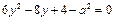 , …………………7分
, …………………7分
已知线段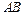 上存在点
上存在点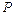 满足
满足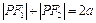 ,即线段
,即线段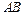 与椭圆
与椭圆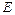 有公共点,
有公共点,
等价于方程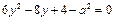 在
在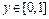 有解. …………………9分
有解. …………………9分
设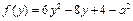 ,
,
∴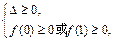 ,解得
,解得
∴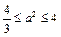 ,
,
故所求的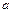 的取值范围是
的取值范围是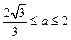 . …………………13分
. …………………13分
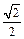 ,故
,故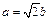 , …………………1分
, …………………1分由
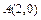 ,得
,得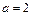 , ∴
, ∴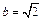 , …………………4分
, …………………4分所以所求的椭圆方程为
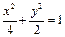 . …………………5分
. …………………5分(Ⅱ)由
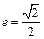 ,可设椭圆方程为
,可设椭圆方程为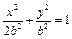 ,
,联立
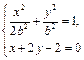 得
得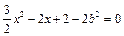 , …………………7分
, …………………7分已知线段
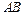 上存在点
上存在点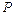 满足
满足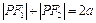 ,即线段
,即线段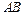 与椭圆
与椭圆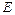 有公共点,
有公共点,等价于方程
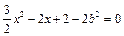 在
在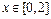 上有解.………………9分
上有解.………………9分∴
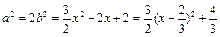 ,
, 由
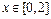 ,故
,故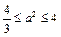 ,
,故所求的
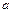 的取值范围是
的取值范围是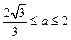 . …………………13分
. …………………13分解法二:(Ⅰ)同解法一;
(Ⅱ)由
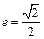 ,设椭圆方程为
,设椭圆方程为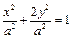 ,
,联立
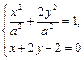 得
得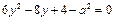 , …………………7分
, …………………7分已知线段
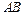 上存在点
上存在点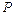 满足
满足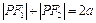 ,即线段
,即线段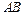 与椭圆
与椭圆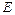 有公共点,
有公共点,等价于方程
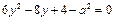 在
在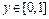 有解. …………………9分
有解. …………………9分设
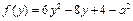 ,
,∴
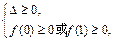 ,解得
,解得
∴
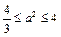 ,
,故所求的
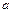 的取值范围是
的取值范围是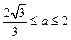 . …………………13分
. …………………13分略

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
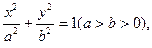 过点A(a,0),B(0,b)的直
过点A(a,0),B(0,b)的直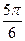 ,原点到该直线的距离为
,原点到该直线的距离为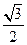 .
.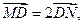 求直线MN的方程;
求直线MN的方程;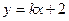 交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。
交椭圆于P、Q两点,以PQ为直径的圆过点D(1,0)?若存在,求出k的值;若不存在,请说明理由。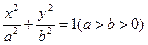 上一点,F1,F2,是椭圆上的两焦点,且满足
上一点,F1,F2,是椭圆上的两焦点,且满足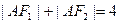
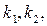 ,若存在常数
,若存在常数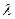 使
使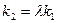 ,求直线CD的斜率.
,求直线CD的斜率. :
: 与抛物线
与抛物线 :
: 的一个交点为M,抛物线
的一个交点为M,抛物线
 ,求
,求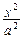 +
+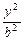 =1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数
=1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数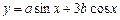 图象的一条对称轴的方程是
图象的一条对称轴的方程是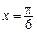 .
. C
C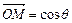
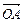 +
+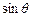
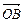 成立.
成立. 的焦点
的焦点

 ,P为椭圆上的一点,已知
,P为椭圆上的一点,已知 ,则△
,则△ 的面积为( )
的面积为( ) 9 B
9 B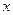 轴上的椭圆
轴上的椭圆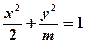 的离心率为
的离心率为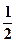 ,则m=( )
,则m=( )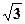
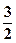
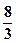
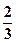
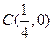 ,椭圆
,椭圆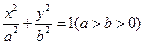 的右准线
的右准线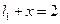 与x轴相交于点D,右焦点F到上顶点的距离为
与x轴相交于点D,右焦点F到上顶点的距离为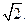
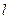 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得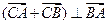 ?若存在,求出直线
?若存在,求出直线