题目内容
12.已知顶点在坐标原点,对称轴为x轴的抛物线C过点P(4,4).(Ⅰ)求抛物线C的标准方程;
(Ⅱ)斜率为$\sqrt{3}$的直线l过抛物线C的焦点F,与抛物线C交于A,B两点,求△AOB的面积(O为坐标原点).
分析 (Ⅰ)设抛物线方程为y2=mx,代入P(4,4),得到方程,解方程即可得到所求抛物线方程.
(Ⅱ)由题意,直线AB方程为y=$\sqrt{3}$(x-1),与y2=4x消去x得:3x2-10x+3=0.再用一元二次方程根与系数的关系和弦长公式,算出|AB|;利用点到直线的距离公式算出点O到直线AB的距离,即可求出△AOB的面积
解答 解:(Ⅰ)设抛物线方程为y2=mx,
代入P(4,4),可得16=4m,即有m=4,
则抛物线的方程为y2=4x;
(Ⅱ)由题意,得直线AB的方程为y=$\sqrt{3}$(x-1),
代入y2=4x得:3x2-10x+3=0
设交点为A(x1,y1),B(x2,y2)
∴x1+x2=$\frac{10}{3}$,x1x2=1
可得|AB|=2|x1-x2|=$\frac{16}{3}$
又∵点O到直线AB的距离d=$\frac{\sqrt{3}}{\sqrt{3+1}}$=$\frac{\sqrt{3}}{2}$,
∴△AOB的面积S△AOB=$\frac{1}{2}$|AB|d=$\frac{1}{2}×\frac{16}{3}×\frac{\sqrt{3}}{2}$=$\frac{4\sqrt{3}}{3}$.
点评 本题考查抛物线的方程的求法,考查待定系数法的运用,考查求焦点弦AB与原点构成的△AOB面积.着重考查了抛物线的定义与简单几何性质、直线与抛物线位置关系等知识,属于中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
2.已知数列{an}的前n项和为Sn,当Sn=n2-n时,a5=( )
| A. | 20 | B. | 12 | C. | 8 | D. | 4 |
3.计算$\frac{i}{1-i}$=-( )
| A. | $\frac{-1+i}{2}$ | B. | $\frac{-1-i}{2}$ | C. | $\frac{1-i}{2}$ | D. | $\frac{1+i}{2}$ |
7. 在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
 在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )
在平行六面体ABCD-A1B1C1D1中,M为AC与BD的交点,若$\overrightarrow{{A}_{1}{B}_{1}}$=$\overrightarrow{a}$,$\overrightarrow{{A}_{1}{D}_{1}}$=$\overrightarrow{b}$,$\overrightarrow{{A}_{1}A}$=$\overrightarrow{c}$,则下列向量中与$\overrightarrow{{B}_{1}M}$相等的向量是( )| A. | -$\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | B. | -$\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | C. | $\frac{1}{2}\overrightarrow{a}$-$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ | D. | $\frac{1}{2}\overrightarrow{a}$+$\frac{1}{2}\overrightarrow{b}$+$\overrightarrow{c}$ |
17.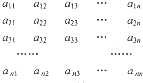 如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )
如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )
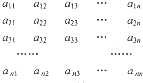 如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )
如图所示,将n2(n≥9)个正数排成n行n列的数阵,其中的每一行都成等差数列,每一列都成等比数列,各等比数列的公比都相同且不为1,若a11=a22=a34=$\frac{1}{2}$,则a11+a22+a33+…+a99=( )| A. | $\frac{1031}{512}$ | B. | $\frac{1031}{512}$ | C. | $\frac{1013}{1024}$ | D. | $\frac{1031}{1024}$ |
