题目内容
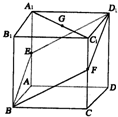
如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别是棱AA1和CC1的中点,G是A1C1的中点,求:
(1)点G到平面BFD1E的距离;
(2)四棱锥A1-BFD1E的体积.
(1)点G到平面BFD1E的距离;
(2)四棱锥A1-BFD1E的体积.

(1)由题得:BE=BF=FD1=ED1=
a,
∴四边形BFD1E是棱形,连接EF和BD1,
有A1C1∥EF,设H是EF中点,
连GH、GD1,则EF⊥GH,EF⊥HD1,
∴EF⊥面GHD1,又EF?面BFD1E中,
∴平面BFD1E⊥平面GHD1,
作GK⊥HD1,则GK⊥面BFD1E,
则G到平面的距离就是KG长.在RT△GHD1中,
GH•GD1=
GK•HD1.
又GH=
a,GD1=
a,HD1=
a,
∴GK=
a.
(2)∵A1C1∥EF,∴A1C1∥平面BFD1E,
∴G到平面BFD1E的距离就是四棱锥A1-BFD1E的高,
∴VA1-BFD1E=
S菱形BFD1E•GK=
•
EF•BD1•GK=
•
a•
a•
a=
a3
| ||
| 2 |
∴四边形BFD1E是棱形,连接EF和BD1,
有A1C1∥EF,设H是EF中点,
连GH、GD1,则EF⊥GH,EF⊥HD1,
∴EF⊥面GHD1,又EF?面BFD1E中,
∴平面BFD1E⊥平面GHD1,
作GK⊥HD1,则GK⊥面BFD1E,
则G到平面的距离就是KG长.在RT△GHD1中,
| 1 |
| 2 |
| 1 |
| 2 |
又GH=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
∴GK=
| ||
| 6 |
(2)∵A1C1∥EF,∴A1C1∥平面BFD1E,
∴G到平面BFD1E的距离就是四棱锥A1-BFD1E的高,
∴VA1-BFD1E=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 6 |
| 1 |
| 6 |

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
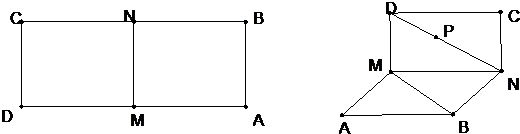
 中,
中, 分别是
分别是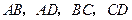 上的点,且直线
上的点,且直线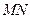 与
与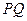 交于点
交于点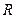 ,求证
,求证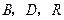 三点共线.
三点共线.