题目内容
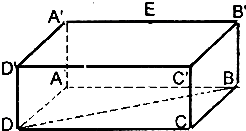
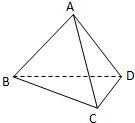
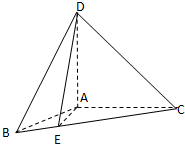
如图，在三棱锥A-BCD中，AD⊥平面ABC，∠BAC=120°，且AB=AC=AD=2，点E在BC上，且AE⊥AC．
（Ⅰ）求证：AC⊥DE；
（Ⅱ）求点B到平面ACD的距离．
（Ⅰ）求证：AC⊥DE；
（Ⅱ）求点B到平面ACD的距离．
（I）∵DA⊥平面ABC，AC?平面ABC，
∴AD⊥AC，…（2分）
∵AE⊥AC，AE、AD是平面ADE内的相交直线，
∴AC⊥平面ADE，
∵DE?平面ADE，∴AC⊥DE．…（6分）
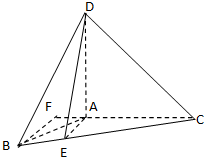
（II）过B点作AC的垂线，垂足为F，
∵DA⊥平面ABC，BF?平面ABC，∴AD⊥BF
∵AC⊥BF，AC、AD是平面ACD内的相交直线，
∴BF⊥平面ACD，
因此BF的长为点B到平面ACD的距离，
在Rt△ABF中，AB=2，∠BAF=180°-120°=60°，
∴BF=ABsin60°=2×
=
，即点B到平面ACD的距离为
．
∴AD⊥AC，…（2分）
∵AE⊥AC，AE、AD是平面ADE内的相交直线，
∴AC⊥平面ADE，
∵DE?平面ADE，∴AC⊥DE．…（6分）
（II）过B点作AC的垂线，垂足为F，
∵DA⊥平面ABC，BF?平面ABC，∴AD⊥BF
∵AC⊥BF，AC、AD是平面ACD内的相交直线，
∴BF⊥平面ACD，
因此BF的长为点B到平面ACD的距离，
在Rt△ABF中，AB=2，∠BAF=180°-120°=60°，
∴BF=ABsin60°=2×
| ||
| 2 |
| 3 |
| 3 |
练习册系列答案
相关题目
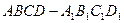中，
、
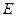分别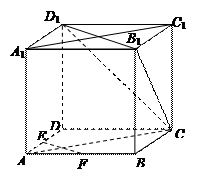
、
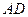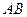的中点．（1）求证：
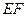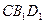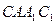∥平面
；
⊥平面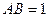
，一个动点从点
、
、
、
、
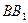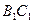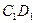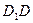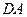上的点，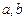
为两条直线，
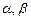为两个平面.下列四个命题中，正确的命题是 ( )
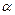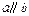
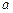
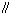
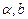
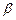
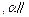
所成的角相等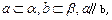，则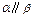
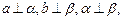则
则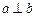
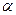的距离依次为a、b、c，且点A与边BC在平面
