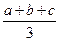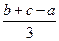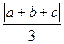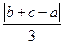题目内容
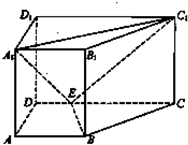
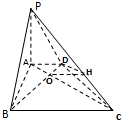
如图示，在底面为直角梯形的四棱椎P-ABCD中，AD∥BC，∠ABC=90°，PA⊥平面ABCD，PA=4，AD=2，AB=2
，BC=6．
（1）求证：BD⊥平面PAC；
（2）求二面角A-PC-D的正切值；
（3）求点D到平面PBC的距离．
| 3 |
（1）求证：BD⊥平面PAC；
（2）求二面角A-PC-D的正切值；
（3）求点D到平面PBC的距离．
（1）证明：令BD与AC相交于点O，
∵在底面为直角梯形的四棱椎P-ABCD中，
AD∥BC，∠ABC=90°，PA⊥平面ABCD，
PA=4，AD=2，AB=2
，BC=6．
∴AC=
=4
，BD=
=4
∵AD∥BC，∴△AOD～△BOC，
∵
=
=
，∴BO=
×4=3，AO=
×4
=
，
∴BO2+AO2=（3）2+（
）2=12=AB2
∴由勾股定理得：BO⊥AC，即：BD⊥AC，又BD⊥PA，AC∩PA=A，
∴BD⊥平面PAC．（3分）
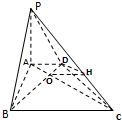
（2）由（1）知：DO⊥平面PAC，
过O作OH⊥PC于H，连DH，则DH⊥PC
则∠DHO就是二面角A-PC-D的平面角，DO=
×BD=
×4=1，
CO=
×AC=
×4
=3
，
在Rt△PAC和Rt△OHC中，
∵∠PAC=∠OHC，∠PCA=∠HCO，∴Rt△PAC～Rt△OHC，
∴
=
，又∵PC=
=8，OH=
．
∴tan∠DHO=
=
，
∴二面角A-PC-D的正切值为
．（7分）
（3）设点D到平面PBC的距离为h，
∵VD-PBC=VP-BDC，
∴
S△PBC•h=
S△BDC•PA=
•[
(2+6)•2
-
×2×2
]•4=8
，
∵BC=6，PB=
=2
，PC=
=8，
∴BC⊥PB，∴S△PBC=
×6×2
=6
，
∴h=
=
．
∴点D到平面PBC的距离为
．
∵在底面为直角梯形的四棱椎P-ABCD中，
AD∥BC，∠ABC=90°，PA⊥平面ABCD，
PA=4，AD=2，AB=2
| 3 |
∴AC=
(2
|
| 3 |
(2
|
∵AD∥BC，∴△AOD～△BOC，
∵
| AD |
| BC |
| 2 |
| 6 |
| 1 |
| 3 |
| 3 |
| 4 |
| 1 |
| 4 |
| 3 |
| 3 |
∴BO2+AO2=（3）2+（
| 3 |
∴由勾股定理得：BO⊥AC，即：BD⊥AC，又BD⊥PA，AC∩PA=A，
∴BD⊥平面PAC．（3分）
（2）由（1）知：DO⊥平面PAC，
过O作OH⊥PC于H，连DH，则DH⊥PC
则∠DHO就是二面角A-PC-D的平面角，DO=
| 1 |
| 4 |
| 1 |
| 4 |
CO=
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 3 |
在Rt△PAC和Rt△OHC中，
∵∠PAC=∠OHC，∠PCA=∠HCO，∴Rt△PAC～Rt△OHC，
∴
| OH |
| PA |
| OC |
| PC |
| PA2+AC2 |
3
| ||
| 2 |
∴tan∠DHO=
| DO |
| OH |
2
| ||
| 9 |
∴二面角A-PC-D的正切值为
2
| ||
| 9 |
（3）设点D到平面PBC的距离为h，
∵VD-PBC=VP-BDC，
∴
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 3 |
∵BC=6，PB=
| 16+12 |
| 7 |
| 16+48 |
∴BC⊥PB，∴S△PBC=
| 1 |
| 2 |
| 7 |
| 7 |
∴h=
8
| ||||
|
4
| ||
| 7 |
∴点D到平面PBC的距离为
4
| ||
| 7 |
练习册系列答案
相关题目
的距离依次为a、b、c，且点A与边BC在平面
